
如图,PA,PB分别与⊙O相切于点A,B,∠APB=60°,连接AO,BO.
(1)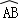 所对的圆心角∠AOB= ;
所对的圆心角∠AOB= ;
(2)求证:PA=PB;
(3)若OA=3,求阴影部分的面积.

科目:初中数学 来源: 题型:
如图,已知∠MON=90°,A是∠MON内部的一点,过点A作AB⊥ON,垂足为点B,AB=3厘米,OB=4厘米,动点E,F同时从O点出发,点E以1.5厘米/秒的速度沿ON方向运动,点F以2厘米/秒的速度沿OM方向运动,EF与OA交于点C,连接AE,当点E到达点B时,点F随之停止运 动.设运动时间为t秒(t>0).
动.设运动时间为t秒(t>0).
(1)当t=1秒时,△EOF与△ABO是否相似?请说明理由;
(2)在运动过程中,不论t取何值时,总有EF⊥OA.为什么?
(3)连接AF,在运动过程中,是否存在某一时刻t,使得S△AEF=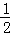 S四边形AEOF?若存在,请求出此时t的值;若不存在,请说明理由.
S四边形AEOF?若存在,请求出此时t的值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,AB是⊙O的直径,弦CD⊥AB于点E,点M在⊙O上,MD恰好经过圆心O,连接MB.
(1)若CD=16,BE=4,求⊙O的直径;
(2)若∠M=∠D,求∠D的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
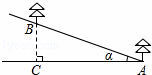
如图,在山坡上植树,已知山坡的倾斜角α是20°,小明种植的两棵树间的坡面距离AB是6米,要求相邻两棵树间的水平距离AC在5.3~5.7米范围内,问小明种植的这两棵树是否符合这个要求?
(参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com