练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

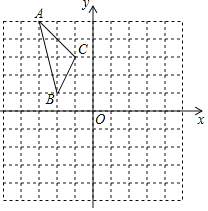
    【题目】如图，在平面直角坐标系中，已知△ABC的三个顶点的坐标分别为A（﹣3，5），B（﹣2，1），C（﹣1，3）．

    （1）若△ABC经过平移后得到△A1B1C1，已知点C的对应点C的坐标为（4，﹣1），画出△A1B1C1并写出顶点A，B对应点A1，B1的坐标；

    （2）将△ABC绕着点O按顺时针方向旋转90°得到△A2B2C2，画出△A2B2C2．

    【答案】（1）作图见解析，A的坐标为（2，1），B的坐标为（3，﹣3）；（2）见解析

    【解析】

    （1）根据点C的对应点C的坐标为（4，﹣1）找到平移规律，画出图形，进而得出坐标即可；

    （2）将三角形三顶点分别绕着点O按顺时针方向旋转90°得到对应点，连接可得．

    ：（1）△ABC如下图所示；A的坐标为（2，1），B的坐标为（3，﹣3）．

    （2）△ABC如下图所示：

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

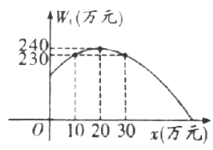
    【题目】某公司计划投资、两种产品，若只投资产品，所获得利润（万元）与投资金额（万元）之间的关系如图所示，若只投资产品，所获得利润（万元）与投资金额（万元）的函数关系式为．

    （1）求与之间的函数关系式；

    （2）若投资产品所获得利润的最大值比投资产品所获得利润的最大值少万元，求的值；

    （3）该公司筹集万元资金，同时投资、两种产品，设投资产品的资金为万元，所获得的总利润记作万元，若时，随的增大而减少，求的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

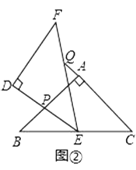
    【题目】△ABC和△DEF是两个全等的等腰直角三角形，∠BAC=∠EDF=90°，△EDF的顶点E与△ABC的斜边BC的中点重合，将△DEF绕点E旋转，旋转过程中，线段DE与线段AB相交于点P，线段EF与射线CA相交于点Q．

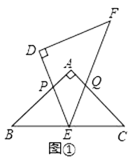
    （1）如图①，当点Q在线段AC上，且AP=AQ时，求证：△BPE≌△CQE；

    （2）如图②，当点Q在线段CA的延长线上时，求证：△BPE∽△CEQ；

    （3）在（2）的条件下，BP=2，CQ=9，则BC的长为_______．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，对△ABC 进行循环往复的轴对称或中心对称变换，若原来点 A 坐标是(a，b)，则经过第 2012 次变换后所得的 A 点坐标是( )

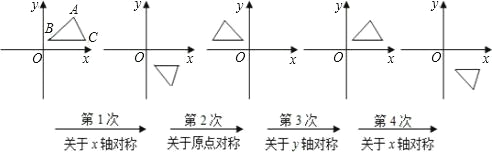
    A. (a，b) B. (a，﹣b) C. (﹣a，b) D. (﹣a，﹣b)

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在直角坐标系中，已知A（0，1），B（10，1），C（9，4）．

    （1）在网格中画出过A、B、C三点的圆和直线的图像；

    （2）已知P是直线上的点，且△APB是直角三角形，那么符合条件的点P共有 个；

    （3）如果直线（k>0）上有且只有二个点Q与点A、点B两点构成直角△ABQ，则k＝ ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】《九章算术》是我国古代数学的经典著作，书中有一个问题：“今有黄金九枚，白银一十一枚，称之重适等．交易其一，金轻十三两．问金、银一枚各重几何？”．意思是：甲袋中装有黄金9枚（每枚黄金重量相同），乙袋中装有白银11枚（每枚白银重量相同），称重两袋相等．两袋互相交换1枚后，甲袋比乙袋轻了13两（袋子重量忽略不计）．问黄金、白银每枚各重多少两？设每枚黄金重x两，每枚白银重y两，根据题意得（　　）

    A.

    B.

    C.

    D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，已知抛物线C1：y＝x2+6x+2的顶点为M，与y轴相交于点N，先将抛物线C1沿x轴翻折，再向右平移p个单位长度后得到抛物线C2，直线l：y＝kx+b经过M，N两点．

    （1）求点M的坐标，并结合图象直接写出不等式x2+6x+2＜kx+b的解集；

    （2）若抛物线C2的顶点D与点M关于原点对称，求p的值及抛物线C2的解析式；

    （3）若抛物线C1与x轴的交点为E、F，试问四边形EMBD是何种特殊四边形？并说明其理由．

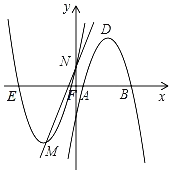
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某校在向贫困地区捐书活动中全体师生积极捐书.为了解所捐书籍的种类，某同学对部分书籍进行了抽样调查，并根据调查数据绘制了如图所示不完整统计图.请根据统计图回答下面问题：

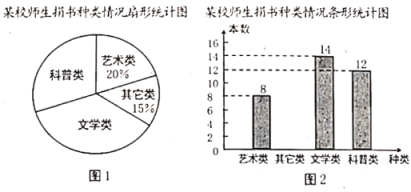
    （1）本次抽样调查的书籍有多少本？请通过计算补全条形统计图；

    （2）求出图中表示科普类书籍的扇形圆心角度数；

    （3）本次活动师生共捐书本，请估计有多少本文学类书籍？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某经销店为某工厂代销一种建筑材料（这里的代销是指厂家先免费提供资源，待货物出售后再进行结算，未出售的由厂家负责处理）。当每吨售价为260元时，月销售量为45吨，该经销店为提高经营利润，准备采取降价的方式进行促销。经市场调查发现：当每吨售价每降低10元时，月销售量就会增加7.5吨，综合考虑各种因素，每售出一吨建筑材料共需支付厂家及其它费用元．

    当每吨售价为元时，月销售量为吨，求出与之间的函数解析式；

    在遵循“薄利多销”的原则下，问每吨材料售价为多少时，该经销店的月利润为元；

    若在规定每吨售价不得超过元的情况下，当每吨售价定为多少元时，经销店的月利润最大．

    查看答案和解析>>

    同步练习册答案