

分析 (1)根据题意可以得到点P表示的实际意义;
(2)根据图形可以得到甲的速度,进而可以求得乙的速度;
(3)根据点P和点Q的坐标,可以求得线段PQ的解析式;
(4)根据图形可以求得线段OP的解析式,然后令线段OP和线段PQ的解析式中的y都等于5,求得x的值,本题得以解决.
解答 解:(1)由题意可得,
当甲到达点B时,两人之间的距离最大,
故答案为:此时甲到达点B;
(2)由题意可得,
甲的速度为:100÷12=$\frac{25}{3}$m/s,
乙的速度为:(200-$13\frac{1}{3}×\frac{25}{3}$)÷$13\frac{1}{3}$=$\frac{20}{3}$m/s;
(3)点P的纵坐标:$\frac{25}{3}×12-\frac{20}{3}×12=20$,
即点P的坐标为(12,20),
设过点P(12,20),Q($13\frac{1}{3}$,0)的线段PQ的解析式为:y=kx+b,
$\left\{\begin{array}{l}{12k+b=20}\\{13\frac{1}{3}k+b=0}\end{array}\right.$
解得,$\left\{\begin{array}{l}{k=-15}\\{b=200}\end{array}\right.$,
即线段PQ的解析式为:y=-15x+200;
(4)设过点O(0,0),P(12,20)的线段OP的解析式为:y=mx,
则12m=20,得m=$\frac{5}{3}$,
即线段OP的解析式为y=$\frac{5}{3}$x,
令$\frac{5}{3}$x=5得x=3,
令-15x+200=5,得x=13,
即从出发到第一次相遇,当x=3或x=13时,甲、乙两人相距5m.
点评 本题考查一次函数的应用,解题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答问题.


 高效智能课时作业系列答案
高效智能课时作业系列答案科目:初中数学 来源: 题型:选择题
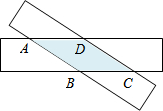 如图,把两条足够长的等宽的纸带交叉放置(不重合),重叠部分形成四边形ABCD,则四边形ABCD是( )
如图,把两条足够长的等宽的纸带交叉放置(不重合),重叠部分形成四边形ABCD,则四边形ABCD是( )| A. | 平行四边形或矩形 | B. | 菱形或正方形 | ||
| C. | 平行四边形或正方形 | D. | 矩形或菱形 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 在平面直角坐标系内xOy中,过双曲线y=$\frac{6}{x}$(x>0)上动点A分别作x轴,y轴的垂线段AB,AC,线段AB,AC与双曲线y=$\frac{k}{x}$(x>,0<k<6)分别交于E,F,记△OEF面积S1,记△AEF的面积为S2,则S=S1-S2的最大值为$\frac{3}{2}$.
在平面直角坐标系内xOy中,过双曲线y=$\frac{6}{x}$(x>0)上动点A分别作x轴,y轴的垂线段AB,AC,线段AB,AC与双曲线y=$\frac{k}{x}$(x>,0<k<6)分别交于E,F,记△OEF面积S1,记△AEF的面积为S2,则S=S1-S2的最大值为$\frac{3}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 肯定没有同一个班级的学生 | |
| B. | 可能有两名同学在一班级,但可能很小 | |
| C. | 至少有三名学生在同一个班级 | |
| D. | 至少有两名学生在同一个班级 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,将四根长度相等的木条首尾相连,钉成四边形ABCD,并转动四边形ABCD使其形状改变,当∠A=60°,测得BD=1,则当∠A=90°时,BD长为( )
如图,将四根长度相等的木条首尾相连,钉成四边形ABCD,并转动四边形ABCD使其形状改变,当∠A=60°,测得BD=1,则当∠A=90°时,BD长为( )| A. | 1 | B. | 2 | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com