
【题目】如图,△ABC在平面直角坐标系中的位置如图所示.
(1)画出△ABC关于y轴对称的△A1B1C1 , 并写出△A1B1C1各顶点坐标;
(2)将△ABC向左平移1个单位,作出平移后的△A2B2C2 , 并写出△A2B2C2的坐标.
科目:初中数学 来源: 题型:
【题目】为了了解我市2017年中考数学学科各分数段成绩分布情况,从中抽取180名考生的中考数学成绩进行统计分析.在这个问题中,样本是指( )
A. 180 B. 被抽取的180名考生
C. 被抽取的180名考生的中考数学成绩 D. 我市2017年中考数学成绩
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等腰△ABC中,
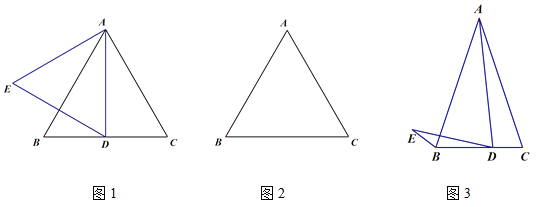
(1)如图1,若△ABC为等边三角形,D为线段BC中点,线段AD关于直线AB的对称线段为线段AE,连接DE,则∠BDE的度数为___________;
(2)若△ABC为等边三角形,点D为线段BC上一动点(不与B,C重合),连接AD并将线段AD绕点D逆时针旋转60°得到线段DE,连接BE.
①根据题意在图2中补全图形;
②小玉通过观察、验证,提出猜测:在点D运动的过程中,恒有CD=BE.经过与同学们的充分讨论,形成了几种证明的思路:
思路1:要证明CD=BE,只需要连接AE,并证明△ADC≌△AEB;
思路2:要证明CD=BE,只需要过点D作DF∥AB,交AC于F,证明△ADF≌△DEB;
思路3:要证明CD=BE,只需要延长CB至点G,使得BG=CD,证明△ADC≌△DEG;
……
请参考以上思路,帮助小玉证明CD=BE.(只需要用一种方法证明即可)
(3)小玉的发现启发了小明:如图3,若AB=AC=kBC,AD=kDE,且∠ADE=∠C,此时小明发现BE,BD,AC三者之间满足一定的的数量关系,这个数量关系是______________________.(直接给出结论无须证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD的度数,下面给出了求∠AGD的度数的过程,将此补充完整并在括号里填写依据. 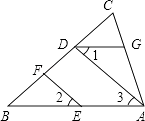
【解】∵EF∥AD(已知)
∴∠2=()
又∵∠1=∠2(已知)
∴∠1=∠3(等式性质或等量代换)
∴AB∥()
∴∠BAC+=180°()
又∵∠BAC=70°(已知)
∴∠AGD=110°(等式性质)
查看答案和解析>>
科目:初中数学 来源: 题型:
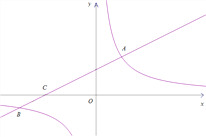
【题目】如图,在平面直角坐标系xOy中,直线![]() 与双曲线
与双曲线![]() 相交于点A(m,3),B(-6,n),与x轴交于点C.
相交于点A(m,3),B(-6,n),与x轴交于点C.
(1)求直线![]() 的解析式;
的解析式;
(2)若点P在x轴上,且![]() ,求点P的坐 标(直接写出结果).
,求点P的坐 标(直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
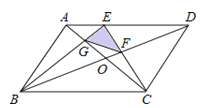
【题目】如图,平行四边形ABCD中,E是AD上的一点,且AE=![]() AD,对角线AC,BD交于点O,EC交BD于F,BE交AC于G,如果平行四边形ABCD的面积为S,那么,△GEF的面积为( )
AD,对角线AC,BD交于点O,EC交BD于F,BE交AC于G,如果平行四边形ABCD的面积为S,那么,△GEF的面积为( )
A. ![]() S B.
S B. ![]() S C.
S C. ![]() S D.
S D. ![]() S
S
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com