
分析 (1)本题涉及绝对值、零指数幂、负整数指数幂3个考点.在计算时,需要针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果;
(2)观察可得最简公分母是2(2x-1),方程两边乘最简公分母,可以把分式方程转化为整式方程求解.
解答 解:(1)|$\sqrt{3}$-1|+20160-(-$\frac{1}{3}$)-1
=$\sqrt{3}$-1+1+3
=$\sqrt{3}$+3;
(2)方程两边乘以2(2x-1)得:3=2x-1,
-2x=-1-3,
-2x=-4,
x=2,
检验:把x=2代入2(2x-1)≠0.
故x=2是原方程的根.
点评 本题主要考查了实数的综合运算能力,是各地中考题中常见的计算题型.解决此类题目的关键是熟练掌握绝对值、零指数幂、负整数指数幂等考点的运算.同时考查了分式方程的解法,注意:(1)解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.(2)解分式方程一定注意要验根.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
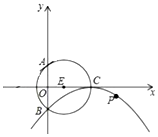 如图,⊙E的圆心E(3,0),半径为5,⊙E与y轴相交于A、B两点(点A在点B的上方),与x轴的正半轴交于点C,直线l的解析式为y=kx+4k+1(k为实数),以点C为顶点的抛物线过点B.
如图,⊙E的圆心E(3,0),半径为5,⊙E与y轴相交于A、B两点(点A在点B的上方),与x轴的正半轴交于点C,直线l的解析式为y=kx+4k+1(k为实数),以点C为顶点的抛物线过点B.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
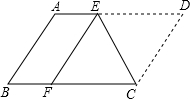 如图,将?ABCD沿CE折叠,使点D落在BC边上的F处,点E在AB上.
如图,将?ABCD沿CE折叠,使点D落在BC边上的F处,点E在AB上.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
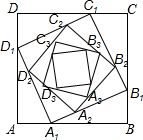 如图,正方形ABCD的边长为a,在AB、BC、CD、DA边上分别取点A1、B1、C1、D1,使AA1=BB1=CC1=DD1=$\frac{1}{3}$a,在边A1B1、B1C1,C1D1、D1A1上分别取点A2、B2、C2、D2,使A1A2、B1B2、C1C2、D1D2=$\frac{1}{3}$A1B1,…,依次规律继续下去,则正方形AnBnCnDn的面积为( )
如图,正方形ABCD的边长为a,在AB、BC、CD、DA边上分别取点A1、B1、C1、D1,使AA1=BB1=CC1=DD1=$\frac{1}{3}$a,在边A1B1、B1C1,C1D1、D1A1上分别取点A2、B2、C2、D2,使A1A2、B1B2、C1C2、D1D2=$\frac{1}{3}$A1B1,…,依次规律继续下去,则正方形AnBnCnDn的面积为( )| A. | $\frac{8}{9}{a}^{2}$ | B. | ($\frac{4}{9}$)na2 | C. | ($\frac{5}{9}$)n-1a2 | D. | ($\frac{5}{9}$)na2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
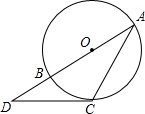 如图,⊙O的直径AB=2,点D在AB的延长线上,DC与⊙O相切于点C,连接AC.若∠A=30°,则CD长为( )
如图,⊙O的直径AB=2,点D在AB的延长线上,DC与⊙O相切于点C,连接AC.若∠A=30°,则CD长为( )| A. | $\frac{1}{3}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\frac{{2\sqrt{3}}}{3}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com