练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，请写出能判定CE∥AB的一个条件_________．

    ∠EBC= ∠B(答案不唯一) 【解析】试题分析：能判定CE∥AB的，判别两条直线平行的方法有：同位角相等，两直线平行；内错角相等，两直线平行；同旁内角互补，两直线平行．因而可以判定的条件是：∠DCE=∠A或∠ECB=∠B或∠A+∠ACE=180°． 【解析】 能判定CE∥AB的一个条件是：∠DCE=∠A或∠ECB=∠B或∠A+∠ACE=180°． 故答案为：∠DCE=∠A（答...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：陕西省2018届九年级上学期期中考试数学试卷 题型：解答题

    （分）如图，点、、、在同一直线上，点、分别在直线的两侧，且， ， ．

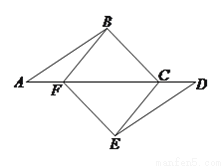
    （1）求证：四边形是平行四边形．

    （）要使四边形为矩形，需要添加一个条件．你可以添加下列条件中的__________．（无需证明）

    ①

    ②

    ③连接，

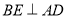
    ④连接，

    （1）见解析；（2）④ 【解析】试题分析：（1）由证得≌，即可得且BC∥EF，即可判定四边形是平行四边形； 根据矩形的判定方法判断即可. 试题解析：(1)证明：∵AF=DC， ∴AC=DF， 在△ABC和△DEF中， ∴△ABC≌△DEF(SAS)， ∴BC=EF，∠ACB=∠DFE， ∴BCEF， ∴四边形是平行四边形； 根据矩形的判定...

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年黑龙江省哈尔滨市双城区七年级（上）期末数学试卷（五四学制） 题型：解答题

    先化简，再求值： （－4x2+2x－8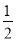）－（x－1），其中x=．

    原式 =,把x=代入原式=. 【解析】试题分析：先去括号，然后合并同类项使整式化为最简，再将x的值代入即可得出答案． 试题解析：原式=﹣x2+x﹣2﹣x+1=﹣x2﹣1， 将x=代入得：﹣x2﹣1=﹣． 故原式的值为：﹣．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年黑龙江省哈尔滨市双城区七年级（上）期末数学试卷（五四学制） 题型：单选题

    8点30分时，时钟的时针与分针所夹的锐角是（ ）

    A．70° B．75° C．80° D．60°

    B． 【解析】 试题分析：钟面每份是30°，8点30分时针与分针相距2．5份，8点30分时，时钟的时针与分针所夹的锐角是30°×2．5=75°，故选B．

    查看答案和解析>>

    科目：初中数学 来源：人教版七年级下册数学第五章相交线与平行线单元检测卷 题型：解答题

    已知：如图，AE⊥BC，FG⊥BC，∠1=∠2，∠D=∠3+60°，∠CBD=70°．

    （1）求证：AB∥CD；

    （2）求∠C的度数．

    （2）25° 【解析】试题分析：（1）求出AE∥GF，求出∠2=∠A=∠1，根据平行线的判定推出即可； （2）根据平行线的性质得出∠D+∠CBD+∠3=180°，求出∠3，根据平行线的性质求出∠C即可． 试题解析：（1）证明： ∵AE⊥BC，FG⊥BC， ∴∠4=∠5=90o． ∴AE∥FG． ∴∠2=∠A． ∵∠1=∠2， ∴∠1=∠A． ...

    查看答案和解析>>

    科目：初中数学 来源：人教版七年级下册数学第五章相交线与平行线单元检测卷 题型：填空题

    如图，BC⊥AC，CB=8cm，AC=6cm，AB=10cm，那么点B到AC的距离是 cm，点A到BC的距离是 cm，C到AB的距离是 cm．

    8，6、4.8． 【解析】 试题分析：如图，过点C作CD⊥AB于点D，则线段CD的长即为点B到AC的距离， ∵BC⊥AC，CB=8cm，AB=10cm，AC=6cm， ∴CD=6×8÷10=4.8cm， 点A到BC的距离是6cm， 点B到AC的距离是8cm．

    查看答案和解析>>

    科目：初中数学 来源：人教版七年级下册数学第五章相交线与平行线单元检测卷 题型：单选题

    如图，已知AB∥CD，∠2＝135°，则∠1的度数是（ ）

    A. 35° B. 45° C. 55° D. 65°

    B 【解析】试题分析：∵AB∥CD，∴∠1=∠3，∵∠2=135°，∴∠3=180°﹣135°=45°，∴∠1=45°，故选B．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年九年级数学北师大版上册 第3章 概率的进一步认识 单元测试卷 题型：填空题

    今年某市中考增加了体育测试科目，考生考试顺序和考试项目(考生从考试的各个项目中抽取一项作为考试项目)由抽签的方式决定，具体操作流程：①每位考生从写有A，B，C的三个小球中随机抽取一个小球确定考试组别；②再从写有“引体向上”“立定跳远”“800米”的抽签纸中抽取一个考试项目进行测试，则考生小明抽到A组“引体向上”的概率是______．

    【解析】试题解析：分别用D，E，F表示“引体向上””立定跳远”“800米”， 画树状图得： ∵共有9种等可能的结果， ∴小明抽到A组“引体向上”的概率=. 故答案为： ．

    查看答案和解析>>

    科目：初中数学 来源：湖南邵阳市区2017-2018学年八年级上册数学期末试卷 题型：解答题

    某公司决定从厂家购进甲、乙两种不同型号的显示器共50台，购进显示器的总金额不超过77000元，已知甲、乙型号的显示器价格分别为1000元/台、2000元/台.

    （1）求该公司至少购买甲型显示器多少台？

    （2）若要求甲型显示器的台数不超过乙型显示器的台数，问有哪些购买方案？

    （1）该公司至少购进甲型显示器23台； （2）购买方案有：①甲型显示器23台，乙型显示器27台； ②甲型显示器24台，乙型显示器26台； ③甲型显示器25台，乙型显示器25台. 【解析】试题分析：（1）设该公司购进甲型显示器x台，则购进乙型显示器（50-x）台，根据两种显示器的总价不超过77000元建立不等式，求出其解即可；（2）由甲型显示器的台数不超过乙型显示器的台数可以建立...

    查看答案和解析>>

    同步练习册答案