
分析 (1)根据去括号、合并同类项,可化简整式;
(2)根据去括号、合并同类项,可化简整式,根据代数式求值,可得答案.
解答 解:(1)原式=5a2+2a-1-12+32a-8a2
=-3a2+34a-13;
(2)原式=3a2b-[2ab2-2ab+3a2b+ab]+3ab2
=3a2b-2ab2+ab-3a2b+3ab2
=ab2+ab,
当a=3,b=-$\frac{1}{3}$时,原式=3×(-$\frac{1}{3}$)2+3×(-$\frac{1}{3}$)
=$\frac{1}{3}$-1
=-$\frac{2}{3}$.
点评 本题考查了整式的化简求值,去括号是解题关键,先去小括号,再去中括号.


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:解答题
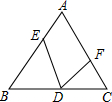 如图,在等边三角形△ABC中,点D为线段BC的中点,点E、F分别在线段AB和AC上,∠EDF=60°.
如图,在等边三角形△ABC中,点D为线段BC的中点,点E、F分别在线段AB和AC上,∠EDF=60°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,一个港湾内有M、N两个小岛,在M岛上的艄公每天早上都要用渡船把M岛上的一部分居民送到OA所在的岸,一部分居民送到OB所在的岸,然后回到N岛上休息,试问:应怎样确定两岸的停泊处,才能使渡船行驶的路程最短?画出图形说明.
如图,一个港湾内有M、N两个小岛,在M岛上的艄公每天早上都要用渡船把M岛上的一部分居民送到OA所在的岸,一部分居民送到OB所在的岸,然后回到N岛上休息,试问:应怎样确定两岸的停泊处,才能使渡船行驶的路程最短?画出图形说明.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 正方形ABCD中,点EF分别在边BC和CD上,且AE⊥BF.点C关于自线BF的对称点为点G,连线FG并延长交AD于点H,若点H是AD的三等分点,则的$\frac{BE}{BC}$值为$\frac{1}{5}$或$\frac{11}{12}$.
正方形ABCD中,点EF分别在边BC和CD上,且AE⊥BF.点C关于自线BF的对称点为点G,连线FG并延长交AD于点H,若点H是AD的三等分点,则的$\frac{BE}{BC}$值为$\frac{1}{5}$或$\frac{11}{12}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com