
【题目】如图,△ABC是等边三角形,点D为BC边上一点,DC=2BD=4,以点D为顶点作正方形DEFG,且DE=BC,连接AE,AG.若将正方形DEFG绕D点旋转一周,当AE取最小值时,AG的长为____

【答案】8
【解析】
点A作AM⊥BC于M,由已知得出BD=2,得出BC=BD+DC=6,由等边三角形的性质得出AB=AC=BC=6,BM=3,得出DM=BMBD=1,在Rt△ABM中,由勾股定理得出AM=![]() ,当正方形DEFG绕点D旋转到点E、A、D在同一条直线上时,AD+AE=DE,即此时AE取最小值,在Rt△ADM中,由勾股定理得出AD=
,当正方形DEFG绕点D旋转到点E、A、D在同一条直线上时,AD+AE=DE,即此时AE取最小值,在Rt△ADM中,由勾股定理得出AD=![]() ,在Rt△ADG中,由勾股定理即可得出AG=8
,在Rt△ADG中,由勾股定理即可得出AG=8
解:过点A作AM⊥BC于M,
∵DC=2BD=4,
∴BD=2,
∴BC=BD+DC=2+4=6,
∵△ABC是等边三角形,
∴AB=AC=BC=6,
∵AM⊥BC,
∴BM=![]() BC=3,
BC=3,
∴DM=BMBD=32=1,
在Rt△ABM中,AM=![]() ,
,
如图,当点E在DA延长线上时,AE=DEAD.
此时AE取最小值,
在Rt△ADM中,AD=![]() ,
,
∵四边形形DEFG是正方形,
∴∠ADG=90°,GD=DE=BC=6,
∴在Rt△ADG中,AG=![]() ,
,
故答案为:8.



科目:初中数学 来源: 题型:
【题目】每年4月23日是世界读书日,某校为了解学生课外阅读情况,随机抽取20名学生,对每人每周用于课外阅读的平均时间(单位:min)进行调查,过程如下:
收集数据:
30 | 60 | 81 | 50 | 40 | 110 | 130 | 146 | 90 | 100 |
60 | 81 | 120 | 140 | 70 | 81 | 10 | 20 | 100 | 81 |
整理数据:
课外阅读平均时间x(min) | 0≤x<40 | 40≤x<80 | 80≤x<120 | 120≤x<160 |
等级 | D | C | B | A |
人数 | 3 | a | 8 | b |
分析数据:
平均数 | 中位数 | 众数 |
80 | m | n |
请根据以上提供的信息,解答下列问题:
(1)填空:a= ,b= ;m= ,n= ;
(2)已知该校学生500人,若每人每周用于课外阅读的平均时间不少于80min为达标,请估计达标的学生数;
(3)设阅读一本课外书的平均时间为260min,请选择适当的统计量,估计该校学生每人一年(按52周计)平均阅读多少本课外书?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是☉
是☉![]() 的直径,
的直径,![]() 为☉
为☉![]() 上一点,
上一点,![]() 是半径
是半径![]() 上一动点(不与
上一动点(不与![]() 重合),过点
重合),过点![]() 作射线
作射线![]() ,分别交弦
,分别交弦![]() ,
,![]() 于
于![]() 两点,过点
两点,过点![]() 的切线交射线
的切线交射线![]() 于点
于点![]() .
.
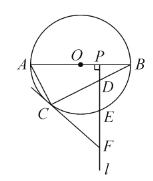
(1)求证:![]() .
.
(2)当![]() 是
是![]() 的中点时,
的中点时,
①若![]() ,判断以
,判断以![]() 为顶点的四边形是什么特殊四边形,并说明理由;
为顶点的四边形是什么特殊四边形,并说明理由;
②若![]() ,且
,且![]() ,则
,则![]() _________.
_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提高学生的阅读能力,我市某校开展了“读好书,助成长”的活动,并计划购置一批图书,购书前,对学生喜欢阅读的图书类型进行了抽样调查,并将调查数据绘制成两幅不完整的统计图,如图所示,请根据统计图回答下列问题:
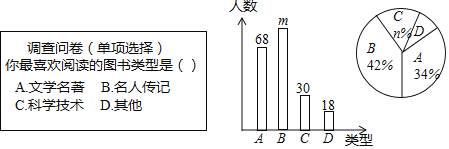
(1)本次调查共抽取了 名学生,两幅统计图中的m= ,n= .
(2)已知该校共有3600名学生,请你估计该校喜欢阅读“A”类图书的学生约有多少人?
(3)学校将举办读书知识竞赛,九年级1班要在本班3名优胜者(2男1女)中随机选送2人参赛,请用列表或画树状图的方法求被选送的两名参赛者为一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将直角三角板![]() 的直角边
的直角边![]() 放在半圆
放在半圆![]() 的直径
的直径![]() 上,直角顶点
上,直角顶点![]() 与直径端点
与直径端点![]() 重合,已知
重合,已知![]() ,且
,且![]() 的直角边
的直角边![]() 与半圆
与半圆![]() 的半径
的半径![]() 长均为2.现将直角三角板
长均为2.现将直角三角板![]() 沿直径
沿直径![]() 的方向向右平移,将三角板
的方向向右平移,将三角板![]() 平移后的三角形记为
平移后的三角形记为![]() .
.
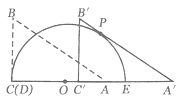
(1)如图,当![]() 平移到斜边与半圆相切时,试求
平移到斜边与半圆相切时,试求![]() 的长度(结果保留
的长度(结果保留![]() );
);
(2)设平移距离为![]() ,在直角三角形
,在直角三角形![]() 平移过程中,折线
平移过程中,折线![]() (包括端点)与半圆弧共有3个交点时,求
(包括端点)与半圆弧共有3个交点时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
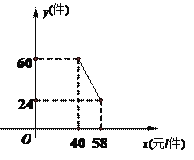
【题目】国家支持大学生创新办实业,提供小额无息贷款,学生王亮享受国家政策贷款36000元用于代理某品牌服装销售,已知该店代理的品牌服装的进价为每件40元,该品牌服装日销售量y(件)与销售价x(元/件)之间的关系可用图中的一条线段(实线)来表示.该店应支付员工的工资为每人每天82元,每天还应支付其它费用为106元(不包含贷款).
(1)求日销售量y(件)与销售价x(元/件)之间的函数关系式;
(2)若该店暂不考虑偿还贷款,当某天的销售价为48元/件时,当天正好收支平衡(销售额-成本=支出),求该店员工的人数;
(3)若该店只有2名员工,则该店至少需要多少天能还清所有贷款?此时每件服装的价格应定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
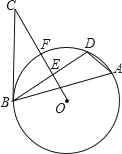
【题目】如图,△ABD是⊙O的内接三角形,E是弦BD的中点,点C是⊙O外一点且∠DBC=∠A,连接OE延长与圆相交于点F,与BC相交于点C.
(1)求证:BC是⊙O的切线;
(2)若⊙O的半径为6,BC=8,求弦BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,![]() 中,
中,![]() 是
是![]() 边上一点,
边上一点,![]() 是
是![]() 的中点,过点
的中点,过点![]() 作
作![]() 的平行线交
的平行线交![]() 的延长线于
的延长线于![]() ,且
,且![]() ,连接
,连接![]() .
.
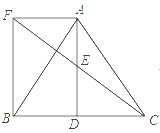
(1)求证:![]() 是
是![]() 的中点;
的中点;
(2)若![]() ,试判断四边形
,试判断四边形![]() 的形状,并证明你的结论.
的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
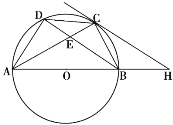
【题目】如图,点A,B,C,D是直径为AB的⊙O上四个点,C是劣弧![]() 的中点,AC交BD于点E,AE=2,EC=1.
的中点,AC交BD于点E,AE=2,EC=1.
(1)求证:△DEC∽△ADC;
(2)连结DO,探究四边形OBCD是否是菱形?若是,请你给予证明;若不是,请说明理由;
(3)延长AB到H,使BH=OB,求证:CH是⊙O的切线.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com