

���� �Ķ����ϣ���ͼ2�У����ۣ�AC=BE+$\frac{1}{2}$AE���������£�ֻҪ֤����ABF�ա�BAC���Ƴ�AC=BF����֤��EF=$\frac{1}{2}$AE���ɵ�AC=BF=BE+EF=BE+$\frac{1}{2}$AE��
���⣺��1���ɡ�ACD=��D+��CAD����D+��CFG=��BAC���Ƴ���CHG=��CFH+��FCH=��CFH+��D+��CAD=��BAC+��CAD=��BAD���ɵá�CHG=��BAD��
��2�����ۣ�AD=FG����ͼ3�У��ӳ�BF��R��ʹ��BR=CD������AR����AJ��CD��EG���ӳ�����J������FJ������֤���ı���ACEJ���ı���AJFR��ƽ���ı��Σ���֤����ABD�ա�JEF����취֤����1=��2�����ɽ�����⣮
��� �⣺�Ķ����ϣ���ͼ2�У����ۣ�AC=BE+$\frac{1}{2}$AE���������£�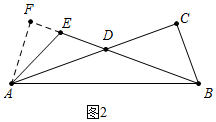
��DA=DB��
���DAB=��DBA��
��AF��BF��
���F=��C=90�㣬
�ڡ�ABF�͡�BAC�У�
$\left\{\begin{array}{l}{��F=��C=90��}\\{��ABF=��BAC}\\{AB=BA}\end{array}\right.$��
���ABF�ա�BAC��
��AC=BF��
�ߡ�AEB=120��=��F+��FAE��
���FAE=30�㣬��EF=$\frac{1}{2}$AE��
��AC=BF=BE+EF=BE+$\frac{1}{2}$AE��
��AC=BE+$\frac{1}{2}$AE��
���⣺��1����ͼ3�У�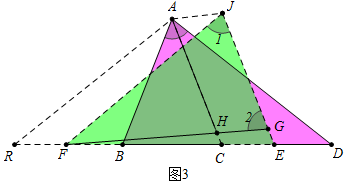
�ߡ�ACD=��D+��CAD����D+��CFG=��BAC��
���CHG=��CFH+��FCH=��CFH+��D+��CAD=��BAC+��CAD=��BAD��
���CHG=��BAD��
��2�����ۣ�AD=FG���������£�
��ͼ3�У��ӳ�BF��R��ʹ��BR=CD������AR����AJ��CD��EG���ӳ�����J������FJ��
��AJ��CE��AC��JE��
���ı���ACEJ���ı���ACGK��ƽ���ı��Σ�
��AJ=CE��AC=JE��
��AB=CA��
��JE=AB��
��AB=AC��
���ABC=��ACB��
���ABR=��ACD��
�ڡ�ABR�͡�ACD�У�
$\left\{\begin{array}{l}{AB=AC}\\{��ABR=��ACD}\\{BR=CD}\end{array}\right.$��
���ABR�ա�ACD��
��AR=AD��
��BR=CD��BF=ED��
��FR=CE=AJ��EF=BD����AJ��RF��
���ı���ARFJ��ƽ���ı��Σ�
��JF=AR=AD��
�ڡ�ABD�͡�JEF�У�
$\left\{\begin{array}{l}{AB=JE}\\{AD=JF}\\{BD=EF}\end{array}\right.$��
���ABD�ա�JEF��
���1=��BAD��
�ߡ�BAD=��CHG=��2��
���1=��2��
��FG=FJ��
��AD=FG��
���� ���⿼�鷭�۱任�����������ε����ʡ�ֱ��������30�Ƚ����ʡ�ȫ�������ε��ж������ʵ�֪ʶ������Ĺؼ���ѧ�����Ӹ����ߣ�����ȫ�������λ������ı��ν�����⣬�����п�ѹ���⣮


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
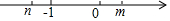 ������m��n�������ϵ�λ����ͼ��ʾ�������ж���ȷ���ǣ�������
������m��n�������ϵ�λ����ͼ��ʾ�������ж���ȷ���ǣ�������| A�� | m��0 | B�� | m��1 | C�� | n��-1 | D�� | n��-1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ������10�����泯�� | B�� | ����5�����泯�� | ||
| C�� | ������8�����泯�� | D�� | ��2�α���1�����泯�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
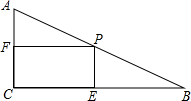 ��ͼ����Rt��ABC�У���C=90�㣬��B=30�㣬AB=12cm������P�ӵ�B��ʼ�ر�BA��2cm/s���ٶ����A�ƶ�������P��PE��BC��PF��AC�����P�ƶ���ʱ��Ϊt���ı���PECF�����ΪS��
��ͼ����Rt��ABC�У���C=90�㣬��B=30�㣬AB=12cm������P�ӵ�B��ʼ�ر�BA��2cm/s���ٶ����A�ƶ�������P��PE��BC��PF��AC�����P�ƶ���ʱ��Ϊt���ı���PECF�����ΪS���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com