列二元一次方程解应用题
为了解决民工子女入学难问题,某市建立了一套民工子女就学的保障机制,其中一项就是免交“借读费”.据统计,2012年秋季有5000名民工子女进入该市中小学学习,预测2013年秋季进入该市中小学学习的民工子女将比2012年有所增加,其中,小学增加20%,中学增加30%,这样,2013年秋季将新增加1160名民工子女在该市中小学学习.
(1)2012年秋季民工子女在小学和中学学习的学生各有多少人?
(2)如果按小学生每年收“借读费”500元,中学生每年收“借读费”1000元计算,求新增的1160名中小学生2013年共免收多少“借读费”?
(3)如果小学生每40名学生配备2名教师,中学生每40名学生配备3名教师,那么按2013年秋季入学后,为民工子女一共需要配备多少名中小学教师?
解:(1)设在小学有x人,在中学有y人,
由题意得,
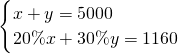
,
解得:

,
答:2012年秋季民工子女在小学学习的学生有3400人,在中学学习的学生有1600人.
(2)新增加的小学生有:20%×3400=680人,新增加的中学生有:30%×1600=480人,
则共免收:500×680+1000×480=820000(元)=82(万元).
答:求新增的1160名中小学生2013年共免收82万元的“借读费”.
(3)2013年秋季入学后,在小学就读的学生有3400×(1+20%)=4080(名),
在中学就读的学生有1600×(1+30%)=2080(名),
则需要老师:(4080÷40)×2+(2080÷40)×3=102×2+52×3=360(名).
答:一共需要配备360名中小学教师.
分析:(1)设在小学有x人,在中学有y人,根据2012年的人数及,新增加的人数,可得出方程组,解出即可;
(2)根据(1)的结果,可计算出免收的“借读费”.
(3)计算出增加后的小学生人数及中学生人数,继而可得出需要的教师数量.
点评:本题考查了二元一次方程组的应用,解题关键是弄清题意,找出合适的等量关系,列出方程组,难度一般.

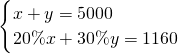 ,
, ,
,
