
【题目】如图,将![]() 绕点
绕点![]() 顺时针旋转得到
顺时针旋转得到![]() ,使点
,使点![]() 的对应点
的对应点![]() 恰好落在边
恰好落在边![]() 上,点
上,点![]() 的对应点为
的对应点为![]() ,连接
,连接![]() ,其中有:①
,其中有:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ,四个结论,则结论一定正确的有( )个
,四个结论,则结论一定正确的有( )个
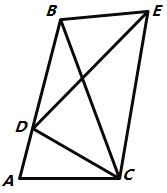
A.1个B.2个C.3个D.4个
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:初中数学 来源: 题型:
【题目】学校与图书馆在冋一条笔直道路上,甲从学校去图书馆,乙从图书馆回学校,甲、乙两人都匀速步行且同时出发,乙先到达日的地.两人之间的距离y(米)与时间t(分钟)之间的函数关系如图所示.
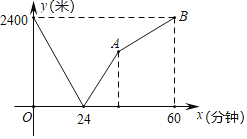
(1)根据图象信息,当t= 分钟时甲乙两人相遇,乙的速度为 米/分钟;
(2)求点A的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、D、C、F在同一条直线上,AD=CF,AB=DE,BC=EF.
(1)求证:ΔABC≌△DEF;
(2)若∠A=55°,∠B=88°,求∠F的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品的进价为每件40元,如果售价为每件50元,每个月可卖出210件;如果售价超过50元但不超过80元,每件商品的售价每上涨1元,则每个月少卖1件;如果售价超过80元后,若再涨价,则每涨1元每月少卖3件.设每件商品的售价为x元,每个月的销售量为y件.
(1)求y与x的函数关系式并直接写出自变量x的取值范围;
(2)设每月的销售利润为W,请直接写出W与x的函数关系式;
(3)每件商品的售价定为多少元时,每个月可获得最大利润?最大的月利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)育德中学800名学生参加第二十届运动会开幕式大型表演,道具选用红黄两色锦绣手幅.已知红色手幅每个4元;黄色手幅每个2.5元;购买800个道具共花费2420元,那么两种手幅各多少个?
(2)学校计划制作1000个吉祥物作为运动会纪念.现有甲、乙两个工厂可以生产这种吉祥物.
甲工厂报价:不超过400个时每个吉祥物20元,400个以上超过部分打七折;但因生产条件限制,截止到学校交货日期只能完成800个;乙工厂报价每个吉祥物18元,但需运费400元.问:学校怎样安排生产可以使总花费最少,最少多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在直角梯形ABCD中,AD∥BC,∠B=∠A=90°,AD=a,BC=b,AB=c,
操作示例
我们可以取直角梯形ABCD的一腰CD的中点P,过点P作PE∥AB,裁掉△PEC,并将△PEC拼接到△PFD的位置,构成新的图形(如图2).
思考发现
小明在操作后发现,该剪拼方法就是先将△PEC绕点P逆时针旋转180°到△PFD的位置,易知PE与PF在同一条直线上.又因为在梯形ABCD中,AD∥BC,∠C+∠ADP=180°,则∠FDP+∠ADP=180°,所以AD和DF在同一条直线上,那么构成的新图形是一个四边形,进而根据平行四边形的判定方法,可以判断出四边形ABEF是一个平行四边形,而且还是一个特殊的平行四边形——矩形.
1.图2中,矩形ABEF的面积是 ;(用含a,b,c的式子表示)
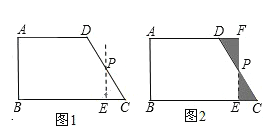
2.类比图2的剪拼方法,请你就图3(其中AD∥BC)和图4(其中AB∥DC)的两种情形分别画出剪拼成一个平行四边形的示意图.
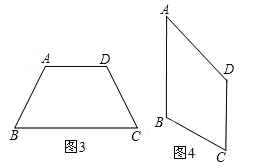
3.小明通过探究后发现:在一个四边形中,只要有一组对边平行,就可以剪拼成平行四边形.
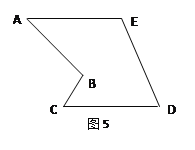
如图5的多边形中,AE=CD,AE∥CD,能否象上面剪切方法一样沿一条直线进行剪切,拼成一个平行四边形?若能,请你在图中画出剪拼的示意图并作必要的文字说明;若不能,简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请阅读下列材料:
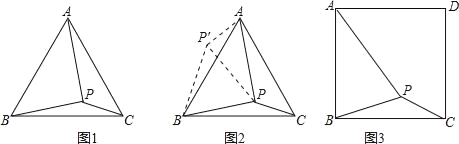
问题:如图1,在等边三角形ABC内有一点P,且PA=2,PB=![]() ,PC=1、求∠BPC度数的大小和等边三角形ABC的边长.
,PC=1、求∠BPC度数的大小和等边三角形ABC的边长.
小刚同学的思路是:将△BPC绕点B逆时针旋转60°,画出旋转后的图形(如图2),连接PP′,可得△P′PC是等边三角形,而△PP′A又是直角三角形(由勾股定理的逆定理可证),所以∠APB=150°,而∠BPC=∠AP′B=150°,进而求出等边△ABC的边长为![]() ,问题得到解决.
,问题得到解决.
请你参考小刚同学的思路,探究并解决下列问题:
如图3,在正方形ABCD内有一点P,且PA=![]() ,BP=2,PC=
,BP=2,PC=![]() .求∠BPC度数的大小和正方形ABCD的边长.
.求∠BPC度数的大小和正方形ABCD的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
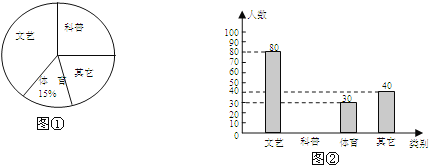
【题目】某校为了进一步丰富学生的课外阅读,欲增购一些课外书,为此对该校一部分学生进行了一次“你最喜欢的书籍”问卷调查(每人只选一项).根据收集到的数据,绘制成如下统计图(不完整):
请根据图中提供的信息,完成下列问题:
(1)在这次问卷调查中,一共抽查了 名学生;并在图中补全条形统计图;
(2)如果全校共有学生1600名,请估计该校最喜欢“科普”书籍的学生约有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com