
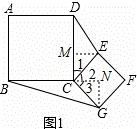
推理证明:如图1,在正方形ABCD和正方形CGFE中,连结DE、BG,设△DCE的面积为S1,△BCG的面积为S2,求证:S1=S2.
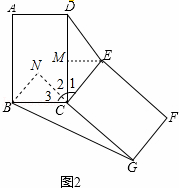
猜想论证:如图2,将矩形ABCD绕点C按顺时针方向旋转后得到矩形FECG,连结DE、BG,设△DCE的面积为S1,△BCG的面积为S2,猜想S1、S2的数量关系,并加以证明.
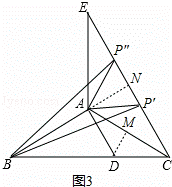
拓展探究:如图3,在△ABC中,AB=AC=10cm,∠B=30°,把△ABC沿AC翻折到△ACE,过点A作AD∥CE交BC于点D,在线段CE上存在点P,使△ABP的面积等于△ACD的面积,请你直接写出CP的长.
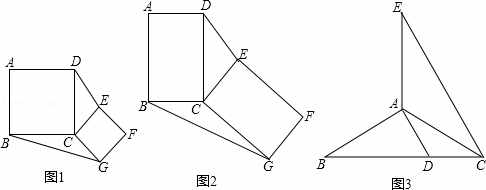
证明:如图1,过点E作EM⊥DC于M点,过点G作GN⊥BC交BC的延长线于N点,
∴∠EMC=∠N=90°,
∵四边形ABCD和四边形ECGF为正方形,
∴∠BCD=∠DCN=∠ECG=90°,CB=CD,CE=CG,
∴∠1=90°﹣∠2,∠3=90°﹣∠2,
∴∠1=∠3.
在△CME和△CNG中
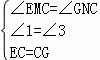
∴△CME≌△CNG(ASA).
∴EM=GN.
又∵S1=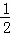 CD•EM,S2=
CD•EM,S2=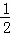 CB•GN,
CB•GN,
∴S1=S2;
猜想论证:
猜想:S1=S2,
证明:如图2,过点E作EM⊥DC于M,过点B作BN⊥GC交GC的延长线于点N,
∴∠EMC=∠N=90°,
∵矩形CGFE由矩形ABCD旋转得到的,
∴CE=CB,CG=CD,
∵∠ECG=∠ECN=∠BCD=90°,
∴∠1=90°﹣∠2,∠3=90°﹣∠2,∴∠1=∠3.
在△CME和△CNB中
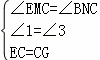
∴△CME≌△CNB(ASA).
∴EM=BN.
又∵S1=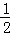 CD•EM,S2=
CD•EM,S2=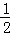 CG•BN,
CG•BN,
∴S1=S2;
拓展探究: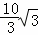 cm或
cm或 cm.
cm.
证明:如图3,作DM⊥AC于M,延长BA,交EC于N,
∵AB=AC=10cm,∠B=30°,
∴∠ACB=∠ABC=30°,
∴∠BAC=120°,
根据对折的性质,∠ACE=∠ACB=30°,
∵AD∥CE,
∴∠DAC=∠ACE=30°,
∴∠BAD=90° ,DM=
,DM=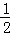 AD,
AD,
∴BN⊥EC,
∵AD=tan∠ABD•AB,AB=10cm,
∴AD=tan30°×10=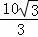 ,
,
∴DM=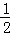 ×
×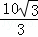 =
=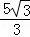 ,
,
∵S△ABP=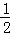 AB•PN,S△ADC=
AB•PN,S△ADC=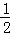 AC•DM,S△ABP=S△ADC,AB=AC,
AC•DM,S△ABP=S△ADC,AB=AC,
∴PN=DM=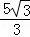 ,
,
在RT△ANC中∠ACN=30°,AC=10cm,
∴NC=cos∠ACN•AC=cos30°×10=5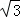 ,
,
∵在EC上到N的距离等于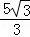 的点有两个,
的点有两个,
∴P′C=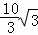 cm,P″C=
cm,P″C=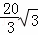 cm,
cm,
∴CP的长为: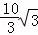 cm或
cm或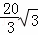 cm.
cm.


 培优口算题卡系列答案
培优口算题卡系列答案科目:初中数学 来源: 题型:
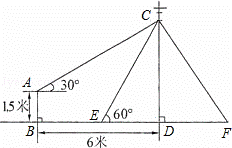
如图,在电线杆上的C处引拉线CE、CF固定电线杆,拉线CE和地面成60°角,在离电线杆6米的B处安置测角仪,在A处测得电线杆上C处的仰角为30°,已知测角仪高AB为1.5米,求拉线CE的长(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在平面直角坐标系中,点A的坐标为(0,3),点B的坐标为(﹣2,0).
(1)把△ABO沿着x轴的正方向平移4个单位,请你画出平移后的△A′B′O′,其中A、B、O的对应点分别是A′、B′、O′(不必写画法);
(2)求△ABO平移前后所扫过的图形的面积S.
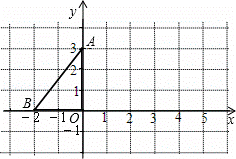
查看答案和解析>>
科目:初中数学 来源: 题型:
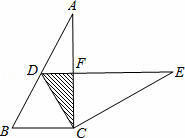
如图,在Rt△ABC中,∠ACB=90°,∠A=30°,BC=2.将△ABC绕点C旋转得到△EDC,使点D在AB边上,斜边DE交AC边于点F,则图中△CDF的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
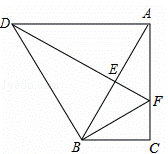
如图,将△ABC绕点B逆时针旋转α得到△DBE,DE的延长线与AC相交于点F,连接DA、BF,∠ABC=α=60°,BF=AF.
(1)求证:DA∥BC;
(2)猜想线段DF、AF的数量关系,并证明你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
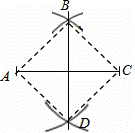
如图,分别以线段AC的两个端点A,C为圆心,大于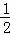 AC的长为半径画弧,两弧相交于B,D两点,连接BD,AB,BC,CD,DA,以下结论:
AC的长为半径画弧,两弧相交于B,D两点,连接BD,AB,BC,CD,DA,以下结论:
①BD垂直平分AC;
②AC平分∠BAD;
③AC=BD;
④四边形ABCD是中心对称图形.
其中正确的有( )
A. ①②③ B.①③④ C.①②④ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
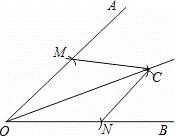
如图,已知∠AOB,按照以下步骤画图:
(1)以O为圆心,适当长为半径画弧,交OA于点M,交OB于点N.
(2)分别以点M、N为圆心,大于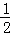 MN的长半径画弧,两弧在∠AOB内部相交于点C.
MN的长半径画弧,两弧在∠AOB内部相交于点C.
(3)作射线OC.
则判断△OMC≌△ONC的依据是( )
A. SAS B.SSS C.ASA D. AAS
查看答案和解析>>
科目:初中数学 来源: 题型:
下列命题是真命题的是( )
①若ac>bc,则a>b;
②抛物线y=x2﹣2x﹣3与坐标轴有2个不同交点;
③对角线相等的菱形是正方形;
④过三点可以作一个圆.
A. ①②③ B.②③ C.③ D. ③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com