
【题目】如图,正△ABC的边长为2,以BC边上的高AB1为边作正△AB1C1,△ABC与△AB1C1公共部分的面积记为S1;再以正△AB1C1边B1C1上的高AB2为边作正△AB2C2,△AB1C1与△AB2C2公共部分的面积记为S2;…,以此类推,则Sn=____.(用含n的式子表示)
【答案】:![]() (
(![]() )n.
)n.
【解析】由AB1为边长为2的等边三角形ABC的高,利用三线合一得到B1为BC的中点,求出BB1的长,利用勾股定理求出AB1的长,进而求出S1,同理求出S2,依此类推,得到Sn.
解:∵等边三角形ABC的边长为2,AB1⊥BC,
∴BB1=1,AB=2,
根据勾股定理得:AB1=![]() ,
,
∴S1=![]() ×
×![]() ×(
×(![]() )2=
)2=![]() (
(![]() )1;
)1;
∵等边三角形AB1C1的边长为![]() ,AB2⊥B1C1,
,AB2⊥B1C1,
∴B1B2=![]() ,AB1=
,AB1=![]() ,
,
根据勾股定理得:AB2=![]() ,
,
∴S2=![]() ×
×![]() ×(
×(![]() )2=
)2=![]() (
(![]() )2;
)2;
依此类推,Sn=![]() (
(![]() )n.
)n.
故答案为:![]() (
(![]() )n.
)n.
“点睛”此题考查了等边三角形的性质,属于规律型试题,熟练掌握等边三角形的性质是解本题的关键.


科目:初中数学 来源: 题型:
【题目】(1)如图所示,已知∠AOB=90°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC,求∠MON的度数;
(2)如果(1)中∠AOB=α,其他条件不变,求∠MON的度数;
(3)如果(1)中∠BOC=β(β为锐角),其他条件不变,求∠MON的度数;
(4)从(1)(2)(3)的结果中你能看出什么规律?

查看答案和解析>>
科目:初中数学 来源: 题型:
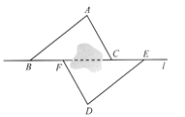
【题目】
如图,点B,F,C,E在直线l上(F,C之间不能直接测量),点A,D在l异侧,测得AB=DE,AC=DF,BF=EC.
(1)求证:△ABC≌△DEF;
(2)指出图中所有平行的线段,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
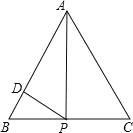
【题目】(2016山东省泰安市第20题)如图,正△ABC的边长为4,点P为BC边上的任意一点(不与点B、C重合),且∠APD=60°,PD交AB于点D.设BP=x,BD=y,则y关于x的函数图象大致是( )
A.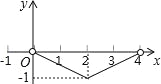 B.
B.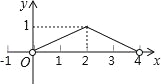
C.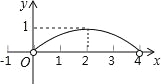 D.
D.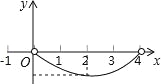
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD中,AB=2,AD=1,∠ADC=60°,将ABCD沿过点A的直线l折叠,使点D落到AB边上的点D′处,折痕交CD边于点E.
(1)求证:四边形BCED′是菱形;
(2)若点P时直线l上的一个动点,请计算PD′+PB的最小值.
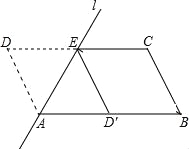
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com