
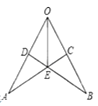
【题目】如图,OE平分∠AOB,BD⊥OA于点D,AC⊥BO于点C,则图中全等三角形共有_______对.
【答案】4
【解析】
根据角平分线定理得到ED=EC,易证Rt△ODE≌△Rt△OCE,Rt△EDA≌Rt△ECB,得到OD=OC,AD=BC,EA=EB,可证出△OAE≌△OBE,△OAC≌△OBD,
①在△DEO与△CEO中,
∵CE⊥AB于点E,BD⊥AC于点D,OE平分∠AOB,
∴∠ODE=∠OCE=90°,∠EOD=∠EOC,
∵OE=OE,
∴△DEO≌△CEO(AAS),
∴OD=OC,DE=CE,
②在△ADE与△BCE中,
∵∠EDA=∠BCE=90°,∠DEA=∠CEB,DE=CE ,
∴△ADE≌△BCE(ASA)
∴AD=BC,AE=BE,∠A=∠B,
∴AC=BD,OA=OB,
③在△AOC与△BOD中,
∵OA=OB,AC=BD,OD=OC
∴△AOC≌△BOD(SSS)
④在△AOE与△BOE中
∵OA=OB,∠AOE=∠BOE,OE=OE,
∴△AOE≌△BOE(SAS)
所以共有四对全等三角形.
故答案为:4


科目:初中数学 来源: 题型:
【题目】如图1,E为矩形ABCD边AD上一点,点P从点B沿折线BE﹣ED﹣DC运动到点C时停止,点Q从点B沿BC运动到点C时停止,它们运动的速度都是1cm/s.若点P,Q同时开始运动,设运动时间为t(s),△BPQ的面积为y(cm2).已知y与t的函数关系图象如图2,有下列四个结论:①AE=6cm;②sin∠EBC= ![]() ;③当0<t≤10时,y=
;③当0<t≤10时,y= ![]() t2; ④当t=12s时,△PBQ是等腰三角形.其中正确结论的序号是 .
t2; ④当t=12s时,△PBQ是等腰三角形.其中正确结论的序号是 . 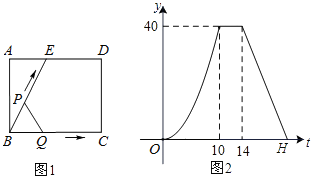
查看答案和解析>>
科目:初中数学 来源: 题型:
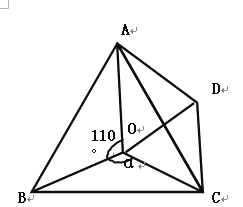
【题目】如图,点0是等边△ABC内一点,∠AOB=110°,∠BOC=α,OC=CD,
且∠DOC=60°连接OD.
(1)求证:△COD是等边三角形
(2)当α=150°时,试判断△AOD的形状,并说明理由
(3)探究:当α为多少度时,△AOD是等腰三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AD是BC边上的高,AE、BF分别是∠BAC、∠ABC的平分线,∠BAC=50°,∠ABC=60°,则∠EAD+∠ACD=( )
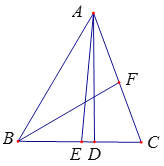
A. 75° B. 80° C. 85° D. 90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,点P为BC边中点,直线a绕顶点A旋转,若点B,P在直线a的异侧,BM⊥直线a于点M.CN⊥直线a于点N,连接PM,PN. 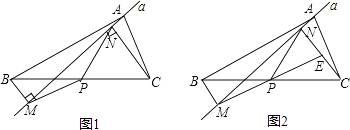
(1)延长MP交CN于点E(如图2). 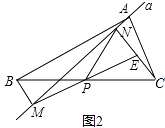
①求证:△BPM≌△CPE;
②求证:PM=PN;
(2)若直线a绕点A旋转到图3的位置时,点B,P在直线a的同侧,其它条件不变,此时PM=PN还成立吗?若成立,请给予证明;若不成立,请说明理由; 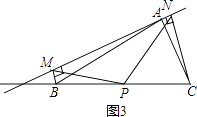
(3)若直线a绕点A旋转到与BC边平行的位置时,其它条件不变,请直接判断四边形MBCN的形状及此时PM=PN还成立吗?不必说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学活动课上,小明提出这样一个问题:∠B=∠C=90°,E是BC的中点,DE平分∠ADC,如图,则下列说法正确的有几个?
(1)AE平分∠DAB;(2)△EBA≌△DCE; (3)AB+CD=AD;(4)AE⊥DE;(5)AB//CD;
大家一起热烈地讨论交流,小红第一个得出正确答案,是( ).
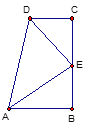
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,OP是∠MON的平分线,请你利用该图形画一对以OP所在直线为对称轴的全等三角形,并将添加的全等条件标注在图上.
请你参考这个作全等三角形的方法,解答下列问题:
(1)如图2,在△ABC中,∠ACB是直角,∠B=60°,AD、CE分别是∠BAC和∠BCA的平分线,AD、CE相交于点F,求∠EFA的度数;
(2)在(1)的条件下,请判断FE与FD之间的数量关系,并说明理由;
(3)如图3,在△ABC中,如果∠ACB不是直角,而( 1 )中的其他条件不变,试问在(2)中所得结论是否仍然成立?若成立,请证明;若不成立,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数y=kx+b图象经过点(1,3)和(4,6)
①试求![]() 与
与![]() ;
;

②画出这个一次函数图象;
③这个一次函数与y轴交点坐标是( )
④当x 时,y<0.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com