
 ∴
∴  ∴AP1=1 ;
∴AP1=1 ; [(4-m)+(5-m)]×2 = 9-2m 1≤m<4;
[(4-m)+(5-m)]×2 = 9-2m 1≤m<4; ∴
∴ 即EC=
即EC=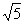
 即m-1=4-
即m-1=4- 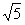 ∴m=5-
∴m=5- 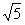
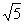 时, ⊙P与⊙E外切;
时, ⊙P与⊙E外切; 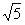 时, ⊙P与⊙E外离;
时, ⊙P与⊙E外离; <m<4时, ⊙P与⊙E相交 。
<m<4时, ⊙P与⊙E相交 。

 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:初中数学 来源: 题型:
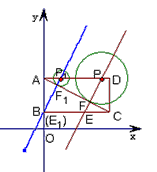
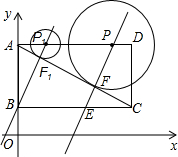 已知,如图,直角坐标系内的矩形ABCD,顶点A的坐标为(0,3),BC=2AB,P为AD边上一动点(与点A、D不重合),以点P为圆心作⊙P与对角线AC相切于点F,过P、F作直线L,交BC边于点E,当点P运动到点P1位置时,直线L恰好经过点B,此时直线的解析式是y=2x+1.
已知,如图,直角坐标系内的矩形ABCD,顶点A的坐标为(0,3),BC=2AB,P为AD边上一动点(与点A、D不重合),以点P为圆心作⊙P与对角线AC相切于点F,过P、F作直线L,交BC边于点E,当点P运动到点P1位置时,直线L恰好经过点B,此时直线的解析式是y=2x+1.查看答案和解析>>
科目:初中数学 来源: 题型:
 已知,如图,直角坐标系内的矩形ABCD,顶点A的坐标为(0,3),BC=2AB,P为
已知,如图,直角坐标系内的矩形ABCD,顶点A的坐标为(0,3),BC=2AB,P为查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:2003年黑龙江省中考数学试卷(解析版) 题型:解答题
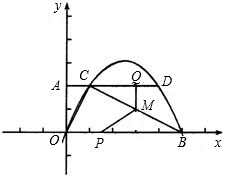
 S梯形AOBC?若存在,请直接写出M点的坐标;若不存在,说明理由.
S梯形AOBC?若存在,请直接写出M点的坐标;若不存在,说明理由.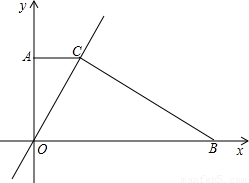
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com