Question

如图，已知：△ABC中，∠C＝Rt∠，AC＝BC，P是AB上任一点．

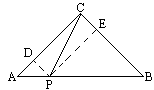
求证：AP²＋BP²＝2PC²．

Answer 1

答案：
解析：

证法一：过P点作PD⊥AC，PE⊥BC，垂足分别为D、E，容易证明 　　AD＝PD，BE＝PE＝CE． 　　在Rt△APD中，AP2＝AD2＋PD2＝2PD2． 　　在Rt△BPE中， 　　BP2＝BE2＋PE2＝2PE2＝2CD2． 　　∴AP2＋BP2＝2PD2＋2CD2＝2(PD2＋CD2)． 　　在Rt△PCD中，PC2＝PD2＋CD2．∴AP2＋BP2＝2PC2． 　　证法二：如图，过C点作CD⊥AB，垂足为D． 　　∵AC＝BC，∠ACB＝Rt∠， 　　∴AD＝BD＝CD． 　　∴AP2＋BP2＝(AD－PD)2＋(BD＋PD)2 　　＝(CD－PD)2＋(CD＋PD)2 　　＝CD2－2CD·PD＋PD2＋CD2＋2CD·PD＋PD2 　　＝2(CD2＋PD2)． 　　在Rt△PDC中，PC2＝CD2＋PD2，AP2＋BP2＝2PC2．

提示：

注：在构造直角二角形证线段的平方和或平方差时，可以发现往往一题有多种处理手段，同学们在平时处理问题的过程中，应加以分析理解，从而达到消化吸收的目的．值得提出的是：方法二中的变换是代数的恒等变形，在几何证明中经常用到，应引起同学们的注意和重视．