
 如图所示,△ABC在平面直角坐标系中,A,B,C的坐标分别是A(-3,3),B(-5,-1),C(-1,1); 点P(m,n)是△ABC内部的一点,平移△ABC,点A、B、C、P的对应点分别是A'、B'、C'、P'.且点P'的坐标为(m+4,n-2).
如图所示,△ABC在平面直角坐标系中,A,B,C的坐标分别是A(-3,3),B(-5,-1),C(-1,1); 点P(m,n)是△ABC内部的一点,平移△ABC,点A、B、C、P的对应点分别是A'、B'、C'、P'.且点P'的坐标为(m+4,n-2).分析 (1)根据网格结构找出点A′、B′、C′的位置,然后顺次连接即可;
(2)将四边形分割成两个三角形,然后利用三角形的面积公式列式计算即可得解;
(3)根据等底等高的三角形面积相等可得点P′与点B到CA′的距离相等,从而确定出点P′的位置,再根据点P′的坐标列出不等式和方程求出m的取值范围,n的值,然后求解即可.
解答 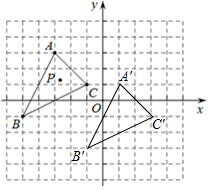 解:(1)△A'B'C'如图所示;
解:(1)△A'B'C'如图所示;
(2)四边形CBB'A'的面积=$\frac{1}{2}$×4×4+$\frac{1}{2}$×2×4,
=8+4,
=12;
(3)∵△CBA'与△CP'A'的面积相等,
∴点P′在经过点C′与x轴平行的△A′B′C′的内部线段上,
∴0<m+4<3,n-2=-1,
解得-4<m<-1,n=1,
∴-3<m+n<0.
故答案为:-3<m+n<0.
点评 本题考查了利用平移作图,三角形的面积,熟练掌握网格结构准确找出对应点的位置是解题的关键.


 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
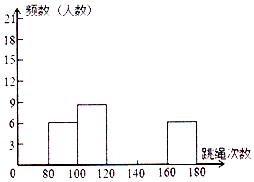 为了进一步了解七年级学生的身体素质情况,体育老师对七(1)班50为学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和频数分布直方图.如图所示.请结合图表完成下列问题:
为了进一步了解七年级学生的身体素质情况,体育老师对七(1)班50为学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和频数分布直方图.如图所示.请结合图表完成下列问题:| 组别 | 次数x | 频数 |
| 第1组 | 80≤x<100 | 6 |
| 第2组 | 100≤x<120 | 8 |
| 第3组 | 120≤x<140 | a |
| 第4组 | 140≤x<160 | 18 |
| 第5组 | 160≤x<180 | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 右转165° | B. | 左转165° | C. | 右转15° | D. | 左转15° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
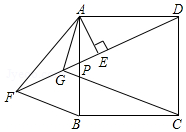 如图,正方形ABCD中,P为AB边上任意一点,AE⊥DP于E,点F在DP的延长线上,且EF=DE,连接AF、BF,∠BAF的平分线交DF于G,连接GC.
如图,正方形ABCD中,P为AB边上任意一点,AE⊥DP于E,点F在DP的延长线上,且EF=DE,连接AF、BF,∠BAF的平分线交DF于G,连接GC.查看答案和解析>>
科目:初中数学 来源:2017届山东泰安市中考二模数学试卷(解析版) 题型:解答题
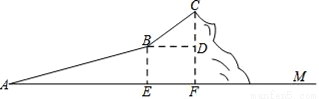
今年“五一”假期.某数学活动小组组织一次登山活动.他们从山脚下A点出发沿斜坡AB到达B点.再从B点沿斜坡BC到达山巅C点,路线如图所示.斜坡AB的长为1040米,斜坡BC的长为400米,在C点测得B点的俯角为30°,点C到水平线AM的距离为600米.
(1)求B点到水平线AM的距离.
(2)求斜坡AB的坡度.
查看答案和解析>>
科目:初中数学 来源:2017届山东泰安市中考二模数学试卷(解析版) 题型:填空题
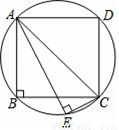
如图,正方形ABCD内接于⊙O,AD=2,弦AE平分BC交BC于P,连接CE,则CE的长为_____________.
查看答案和解析>>
科目:初中数学 来源:2017届广东省揭阳市九年级下学期第一次月考数学试卷(解析版) 题型:解答题
已知关于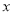 的一元二次方程
的一元二次方程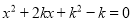 有两个不相等的实数根.
有两个不相等的实数根.
(1)求实数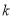 的取值范围;
的取值范围;
(2)0可能是方程一个根吗?若是,求出它的另一个根;若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 36 | B. | ±6 | C. | 6 | D. | $±\sqrt{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com