练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】（1）解方程：x2﹣5x﹣6＝0

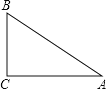
    （2）如图，△ABC中∠C＝90°

    ①将△ABC绕A点逆时针旋转90°，画出旋转后的三角形△AB′C′；

    ②若BC＝3，AC＝4，B点旋转后的对应是B′，求 的长

    【答案】（1）x1＝6，x2＝﹣1．（2）．

    【解析】

    （1）根据十字相乘法可求出x的两个值.

    （2）①△ABC绕A点逆时针旋转90°，画图时注意A点保持不变，AB边沿点A逆时针旋转90°得到，AC边沿点A逆时针旋转90°得到,连接，△AB′C′即为所求.

    ②根据勾股定理可求出斜边AB的长度，由于圆心角，根据弧长公式可求出的长.

    解：（1）解方程：x2﹣5x﹣6＝0

    （x﹣6）（x+1）＝0

    x1＝6，x2＝﹣1．

    （2）①如图所示：

    △AB′C′即为旋转后的三角形；

    ②△ABC中，∠C＝90°

    根据勾股定理，得

    ,

    旋转角为90°，即∠BAB′＝90°．

    ∴.

    答：的长为．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图是一个转盘．转盘分成8个相同的图形，颜色分为红、绿、黄三种．指针的位置固定，转动转盘后任其兹有停止，其中的某个扇形会恰好停在指针所指的位置(指针指向两个图形的交线时，当作指向右边的图形)．求下列事件的概率：

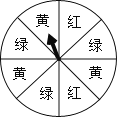
    （1）指针指向红色；

    （2）指针指向黄色或绿色。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知双曲线y1=与直线y2=ax+b交于点A（﹣4，1）和点B（m，﹣4）．

    （1）求双曲线和直线的解析式；

    （2）直接写出线段AB的长和y1＞y2时x的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

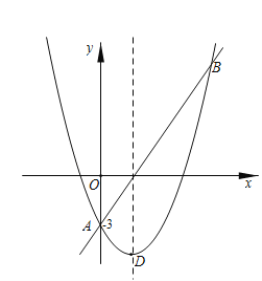
    【题目】如图，直线AB和抛物线的交点是A（0，﹣3），B（5，9），已知抛物线的顶点D的横坐标是2．

    （1）求抛物线的解析式及顶点坐标；

    （2）在x轴上是否存在一点C，与A，B组成等腰三角形？若存在，求出点C的坐标，若不在，请说明理由；

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】我们将能完全覆盖某平面图形的最小圆称为该平面图形的最小覆盖圆．例如线段AB的最小覆盖圆就是以线段AB为直径的圆．

    （1）请分别作出下图中两个三角形的最小覆盖圆（要求用尺规作图，保留作图痕迹，不写作法）；

    （2）探究三角形的最小覆盖圆有何规律？请写出你所得到的结论（不要求证明）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AB是⊙O的直径，AM和BN是⊙O的两条切线，E为⊙O上一点，过点E作直线DC分别交AM，BN于点D，C，且CB=CE．

    （1）求证：DA=DE；

    （2）若AB=6，CD=4，求图中阴影部分的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

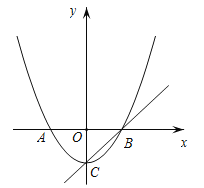
    【题目】如图，已知顶点为的抛物线与轴交于，两点，直线过顶点和点．

    （1）求的值；

    （2）求函数的解析式；

    （3）抛物线上是否存在点，使得？若存在，求出点的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】我们知道：任何有理数的平方都是一个非负数，即对于任何有理数a，都有 成立，所以，当时，有最小值0.

    （应用）：（1）代数式有最小值时， ；

    （2）代数式的最小值是 ；

    （探究）：求代数式的最小值，小明是这样做的：

    ∴当时，代数式有最小值，最小值为5．

    （3）请你参照小明的方法，求代数式的最小值，并求此时a的值．

    （拓展）：（4）若，直接写出y的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系中，A(t，0)，B(t+2，0).对于线段AB和点P给出如下定义：当∠APB＝90°时，称点P为线段AB的“直角点”.

    (Ⅰ)当t＝﹣1时，点C(0，1)，判断点C是否为线段AB的“直角点”，并说明理由；

    (Ⅱ)已知抛物线y＝ax2+bx(a＞0，b＜0)的顶点为M，与x轴交于A(t，0)，B(t+2，0)，若点M为线段AB的“直角点”，求出此抛物线的解析式.

    查看答案和解析>>

    同步练习册答案