
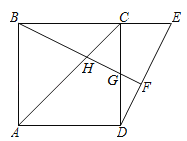
【题目】如图,点E是正方形ABCD的边BC延长线上一点,连结DE,过顶点B作BF⊥DE,垂足为F,BF分别交AC于H,交BC于G.
(1)求证:BG=DE;
(2)若点G为CD的中点,求![]() 的值.
的值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)由于BF⊥DE,所以∠GFD=90°,从而可知∠CBG=∠CDE,根据全等三角形的判定即可证明△BCG≌△DCE,从而可知BG=DE;
(2)设CG=1,从而知CG=CE=1,由勾股定理可知:DE=BG=![]() ,由易证△ABH∽△CGH,所以
,由易证△ABH∽△CGH,所以![]() =2,从而可求出HG的长度,进而求出
=2,从而可求出HG的长度,进而求出![]() 的值.
的值.
试题解析:(1)∵BF⊥DE,∴∠GFD=90°,∵∠BCG=90°,∠BGC=∠DGF,∴∠CBG=∠CDE,在△BCG与△DCE中,∵∠CBG=∠CDE,BC=CD,∠BCG=∠DCE,∴△BCG≌△DCE(ASA),∴BG=DE;
(2)设CG=1,∵G为CD的中点,∴GD=CG=1,由(1)可知:△BCG≌△DCE(ASA),∴CG=CE=1,∴由勾股定理可知:DE=BG=![]() ,∵sin∠CDE=
,∵sin∠CDE=![]() ,∴GF=
,∴GF=![]() ,∵AB∥CG,∴△ABH∽△CGH,∴
,∵AB∥CG,∴△ABH∽△CGH,∴![]() ,∴BH=
,∴BH=![]() ,GH=
,GH=![]() ,∴
,∴![]() =
=![]() .
.


科目:初中数学 来源: 题型:
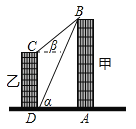
【题目】如图,线段AB、CD分别表示甲乙两建筑物的高,BA⊥AD,CD⊥DA,垂足分别为A、D.从D点测到B点的仰角α为60°,从C点测得B点的仰角β为30°,甲建筑物的高AB=30米
(1)求甲、乙两建筑物之间的距离AD.
(2)求乙建筑物的高CD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人由相距60km的两地同时出发相向而行,甲步行每小时走5km,乙骑自行车,3h后相遇,则乙的速度为( )
A. 5 km/hB. 10 km/hC. 15 km/hD. 20 km/h
查看答案和解析>>
科目:初中数学 来源: 题型:
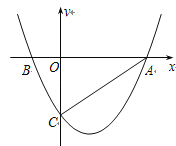
【题目】如图,抛物线![]() 与x轴交于A、B两点,与y轴交于C点,已知A(3,0),且M(1,
与x轴交于A、B两点,与y轴交于C点,已知A(3,0),且M(1,![]() )是抛物线上另一点.
)是抛物线上另一点.
(1)求a、b的值;
(2)连结AC,设点P是y轴上任一点,若以P、A、C三点为顶点的三角形是等腰三角形,求P点的坐标;
(3)若点N是x轴正半轴上且在抛物线内的一动点(不与O、A重合),过点N作NH∥AC交抛物线的对称轴于H点.设ON=t,△ONH的面积为S,求S与t之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场把一个双肩背书包按进价提高50%标价,然后再按八折出售,这样商场每卖出一个书包就可赢利8元.设每个双肩背书包的进价是x元,根据题意列一元一次方程,正确的是( )
A.(1+50%)x80%﹣x=8
B.50%x80%﹣x=8
C.(1+50%)x80%=8
D.(1+50%)x﹣x=8
查看答案和解析>>
科目:初中数学 来源: 题型:
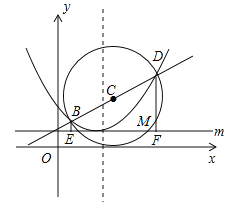
【题目】如图,已知抛物线![]() (a≠0)的图象的顶点坐标是(2,1),并且经过点(4,2),直线
(a≠0)的图象的顶点坐标是(2,1),并且经过点(4,2),直线![]() 与抛物线交于B,D两点,以BD为直径作圆,圆心为点C,圆C与直线m交于对称轴右侧的点M(t,1),直线m上每一点的纵坐标都等于1.
与抛物线交于B,D两点,以BD为直径作圆,圆心为点C,圆C与直线m交于对称轴右侧的点M(t,1),直线m上每一点的纵坐标都等于1.
(1)求抛物线的解析式;
(2)证明:圆C与x轴相切;
(3)过点B作BE⊥m,垂足为E,再过点D作DF⊥m,垂足为F,求MF的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com