
分析 根据配方法的步骤先移项,再两边都除以2,再配方,最后开方即可得出答案.
解答 解:2x2-4x=5,
x2-2x=$\frac{5}{2}$,
x2-2x+1=$\frac{5}{2}$+1,即(x-1)2=$\frac{7}{2}$,
∴x-1=±$\frac{\sqrt{14}}{2}$,
x=1±$\frac{\sqrt{14}}{2}$,
∴x1=$\frac{2+\sqrt{14}}{2}$,x2=$\frac{2-\sqrt{14}}{2}$.
点评 本题主要考查配方法解一元二次方程,用配方法解一元二次方程的步骤:
①把原方程化为ax2+bx+c=0(a≠0)的形式;②方程两边同除以二次项系数,使二次项系数为1,并把常数项移到方程右边;③方程两边同时加上一次项系数一半的平方;④把左边配成一个完全平方式,右边化为一个常数;⑤如果右边是非负数,就可以进一步通过直接开平方法来求出它的解,如果右边是一个负数,则判定此方程无实数解..


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
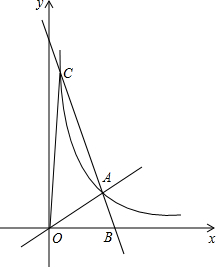 如图,在平面直角坐标系xOy中,直径OA与双曲线y=$\frac{m}{x}$在第一象限内交于点A,过点A的直线y=kx+b与x轴正半轴交于点B,与双曲线的另一交点为C,连接OC.已知OA=OB=5,sin∠AOB=$\frac{3}{5}$.
如图,在平面直角坐标系xOy中,直径OA与双曲线y=$\frac{m}{x}$在第一象限内交于点A,过点A的直线y=kx+b与x轴正半轴交于点B,与双曲线的另一交点为C,连接OC.已知OA=OB=5,sin∠AOB=$\frac{3}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com