
����Ŀ����ͼ��ƽ���ı��� ABCD ����AD��BC��AB=BC=CD=AD=4����A=��C=60�������� BD������BCD �Ƶ� B ��ת���� BD���� BD�䣩�� AD ����һ�� E��BC���� BC����ͬʱ�� CD ����һ�� F ʱ�����н�����ȷ���ǣ� ��
��AE=DF���ڡ�BEF=60�㣻�ۡ�DEB=��DFB���ܡ�DEF ���ܳ�����Сֵ��4+2![]()
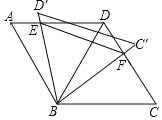
A. �٢� B. �ڢ� C. �٢ڢ� D. �٢ڢۢ�
���𰸡�C
��������
���������֤��ABE�ա�BDF�����жϢ٢ڢ����ɡ�DEF���ܳ�=DE+DF+EF=AD+EF=4+EF����EF��Сʱ��DEF���ܳ���С�����ݴ��߶�������ɵ�BE��ADʱ��BE��С����EF��С���������ʱ��BDE�ܳ���Сֵ��
��AB=BC=CD=AD=4����A=��C=60�㣬
���ABD����BCDΪ�ȱ������������A=��BDC=60�㣮
�߽���BCD�Ƶ�B��ת����BC'D'λ����
���ABD'=��DBC'����AB=BD����A=��DBC'��
���ABE�ա�BFD��
��AE=DF��BE=BF����AEB=��BFD��
���BED+��BFD=180�㣮
�ʢ���ȷ���۴�����
�ߡ�ABD=60�㣬��ABE=��DBF��
���EBF=60�㣮
�ʢ���ȷ��
�ߡ�DEF���ܳ�=DE+DF+EF=AD+EF=4+EF��
�൱EF��Сʱ���ߡ�DEF���ܳ���С��
�ߡ�EBF=60�㣬BE=BF�����BEF�ǵȱ���������
��EF=BE��
�൱BE��ADʱ��BE������С����EF������С��
��AB=4����A=60�㣬BE��AD��
��EB=2![]() ��
��
���DEF���ܳ���СֵΪ4+2![]() ��
��
�ʢ���ȷ��
��ѡC��


 Сѧ������ҵϵ�д�
Сѧ������ҵϵ�д� ��ʿһ��ȫͨϵ�д�
��ʿһ��ȫͨϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����(![]() +2)(
+2)(![]() ��2)��1��
��2)��1��![]()
![]() ��a(a��0)��(
��a(a��0)��(![]() +1)(
+1)(![]() ��1)��b��1(b��0)�����������ж��θ�ʽ�Ĵ���ʽ��ˣ��������ж��θ�ʽ�����dz�����������ʽ��Ϊ��������ʽ�����磬
��1)��b��1(b��0)�����������ж��θ�ʽ�Ĵ���ʽ��ˣ��������ж��θ�ʽ�����dz�����������ʽ��Ϊ��������ʽ�����磬![]() ��
��![]() ��
��![]() +1��
+1��![]() ��1��2
��1��2![]() +3
+3![]() ��2
��2![]() ��3
��3![]() �ȶ��ǻ�Ϊ��������ʽ�����ж��θ�ʽ����ʱ��������������ʽ�����Ի�ȥ��ĸ�еĸ��ţ�������������⣺
�ȶ��ǻ�Ϊ��������ʽ�����ж��θ�ʽ����ʱ��������������ʽ�����Ի�ȥ��ĸ�еĸ��ţ�������������⣺
(1)����![]() ��
��
(2)���㣺![]() ��
��
(3)�Ƚ�![]() ��
��![]() �Ĵ�С����˵�����ɣ�
�Ĵ�С����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һ�κ���y=kx+b��ͼ����A(3,0),��y�ύ�ڵ�B,����AOB�����Ϊ6,��y��x���������С,�������һ�κ����Ľ���ʽ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ȫ�������ů���£�Щ�����ڻ�����ʧ���ڱ���|��ʧ12���һ�ֵ͵�ֲ��̦���Ϳ�ʼ����ʯ��������ÿһ��̦���᳤�ɽ��Ƶ�Բ����̦��ֱ���������������Ƶ��������µĹ�ϵʽ��d=7![]() (t��12)������d��ʾ̦��ֱ������λ�����ף�t����������ʧ��ʱ��(��λ����)��
(t��12)������d��ʾ̦��ֱ������λ�����ף�t����������ʧ��ʱ��(��λ����)��
(1)���������ʧ16���̦��ֱ��Ϊ��������?
(2)������һЩ̦��ֱ����35���ף��ʱ���Լ���ڶ�����ǰ��ʧ��?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����BAD���ɡ�BEC��ƽ�����Ƶ�B��ת60����ã���AB��BC��BE=CE������DE�� 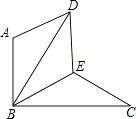
��1����֤����BDE�ա�BCE��
��2�����ж��ı���ABED����״����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AC��ƽ���ı���ABCD�ĶԽ��ߣ�E��H�ֱ�Ϊ��BA�ͱ�BC�ӳ����ϵĵ㣬����EH��AD��CD�ڵ�F��G����EH��AC��
��1����֤��EG=FH��
��2������ACD�ǵ���ֱ�������Σ���ACD=90�㣬F��AD���е㣬AD=6������BF����BF�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���y=kx+b��ͼ���뷴��������y= ![]() ��ͼ���ڵ�A�v��2����5�wC�v5��n�w����y���ڵ�B����x���ڵ�D��
��ͼ���ڵ�A�v��2����5�wC�v5��n�w����y���ڵ�B����x���ڵ�D�� 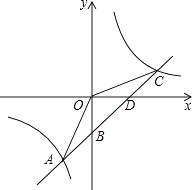
��1����������y= ![]() ��һ�κ���y=kx+b�ı���ʽ��
��һ�κ���y=kx+b�ı���ʽ��
��2������OA��OC�����AOC���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ⲻ��ʽ
��1�����㣺��3���У�0+2tan60��+����1��2015�� ![]() ��
��
��2���ⲻ��ʽ�飺 ![]() ���������Ľ��������ϱ�ʾ������
���������Ľ��������ϱ�ʾ������ ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�AB=AC����DΪBC��һ�㣬��AD=DC����A��B��D��������O��AE�ǡ�O��ֱ��������DE�� 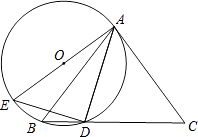
��1����֤��AC�ǡ�O�����ߣ�
��2����sinC= ![]() ��AC=6�����O��ֱ����
��AC=6�����O��ֱ����
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com