

 吨,缴纳水费为
吨,缴纳水费为 元,试列出
元,试列出 与
与 的函数式;
的函数式; 元的取值范围为
元的取值范围为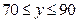 ,试求
,试求 的取值范围。
的取值范围。 优学名师名题系列答案
优学名师名题系列答案科目:初中数学 来源:不详 题型:解答题
 ,求此时直线PM的解析式;
,求此时直线PM的解析式; ,PM的延长线与CD的延长线交于点F,若三角形G
,PM的延长线与CD的延长线交于点F,若三角形G F的面积为4,求此时直线PM的解析式;
F的面积为4,求此时直线PM的解析式;
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 元;一月用水超过10吨的用户,10吨水仍按每吨
元;一月用水超过10吨的用户,10吨水仍按每吨 元收费,超过10吨的部分,按每吨
元收费,超过10吨的部分,按每吨 元(
元( )收费.设一户居民月用水
)收费.设一户居民月用水 吨,应收水费
吨,应收水费 元,
元, 与
与 之间的函数关系如图所示.
之间的函数关系如图所示.
 的值,若某户居民上月用水8吨,则应收水费多少元?
的值,若某户居民上月用水8吨,则应收水费多少元? 的值,并写出当
的值,并写出当 时,
时, 与
与 之间的函数关系式;
之间的函数关系式;查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
| 月份x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 价格y1(元/件) | 560 | 580 | 600 | 620 | 640 | 660 | 680 | 700 | 720 |

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com