
【题目】如图所示,某公司员工分别住在A,B,C三个住宅区,A区有30人,B区有15人,C区有10人.三个区在同一条直线上,该公司的接送车打算在此间设一个停靠点,为使所有员工步行到停靠点的路程之和最小,那么停靠点的位置应设在哪个区?
![]()
【答案】停靠点的位置应设在A区.
【解析】根据题意分别计算停靠点分别在各点是员工步行的路程和,选择最小的即可解
解:所有员工步行到停靠点A区的路程之和为:
0×30+100×15+(100+200)×10
=0+1 500+3 000=4 500(m);
所有员工步行到停靠点B区的路程之和为:
100×30+0×15+200×10
=3 000+0+2 000=5 000(m);
所有员工步行到停靠点C区的路程之和为:
(100+200)×30+15×200+10×0
=9 000+3 000+0=12 000(m).
因为4 500<5 000<12 000,所以所有员工步行到停靠点A区的路程之和最小,故停靠点的位置应设在A区.
“点睛”此题考查了比较线段的长短,正确理解题意是解题的关键.要能把线段的概念在现实中进行应用.


 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
【题目】有两根木条,一根AB长为80 cm,另一根CD长为130 cm,在它们的中点处各有一个小圆孔M,N(圆孔直径忽略不计,M,N抽象成两个点),将它们的一端重合,放置在同一条直线上,此时两根木条的小圆孔之间的距离MN是多少?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
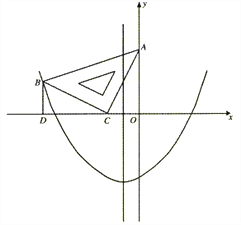
【题目】在平面直角坐标系中,现将一块等腰直角三角板ABC放在第二象限,斜靠在两坐标轴上,点C为 (-1,0) .如图所示,B点在抛物线y=![]() x2+
x2+![]() x-2图象上,过点B作BD⊥x轴,垂足为D,且B点横坐标为-3.
x-2图象上,过点B作BD⊥x轴,垂足为D,且B点横坐标为-3.
(1)求证:△BDC≌△COA;
(2)求BC所在直线的函数关系式;
(3)抛物线的对称轴上是否存在点P,使△ACP是以AC为直角边的直角三角形?若存在,求出所有点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校研究性学习小组在学习二次根式![]() =|a|之后,研究了如下四个问题,其中错误的是( )
=|a|之后,研究了如下四个问题,其中错误的是( )
A. 在a>1的条件下化简代数式a+![]() 的结果为2a﹣1
的结果为2a﹣1
B. 当a+![]() 的值恒为定值时,字母a的取值范围是a≤1
的值恒为定值时,字母a的取值范围是a≤1
C. a+![]() 的值随a变化而变化,当a取某个数值时,上述代数式的值可以为
的值随a变化而变化,当a取某个数值时,上述代数式的值可以为![]()
D. 若![]() =(
=(![]() )2,则字母a必须满足a≥1
)2,则字母a必须满足a≥1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若A与B都是二次多项式,则A﹣B:(1)一定是二次式;(2)可能是四次式;(3)可能是一次式;(4)可能是非零常数;(5)不可能是零.上述结论中,不正确的有( )个.
A. 5 B. 4 C. 3 D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)10-8÷(-2)3+(-4)2×(-2);
(2)(-![]() )×(-22+1
)×(-22+1![]() -
-![]() );
);
(3)(-2)3-[(-3)2-22×![]() -8
-8![]() ]÷(-
]÷(-![]() )2.
)2.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com