
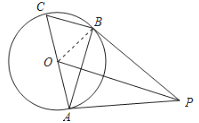
【题目】如图,AC是⊙O的直径,BC是⊙O的弦,点P是⊙O外一点,连接PA,PB,AB,已知∠PBA=∠C.

(1)求证:PB是⊙O的切线;
(2)连接OP,若OP∥BC,且OP=8,⊙O的半径为![]() ,求BC的长.
,求BC的长.
【答案】(1)详见解析;(2)2.
【解析】
试题分析:(1)连接OB,由AC是⊙O的直径可得∠ABC=90°,∠C+∠BAC=90°.再由OA=OB可得∠BAC=∠OBA. 又因∠PBA=∠C,所以∠PBA+∠OBA=90°,即PB⊥OB.即可判定PB是⊙O的切线.(2)可证△ABC∽△PBO,根据相似三角形的性质即可求BC的长.
试题解析: (1)证明:如图所示,连接OB.
∵AC是⊙O的直径,
∴∠ABC=90°,∠C+∠BAC=90°.
∵OA=OB,
∴∠BAC=∠OBA.
∵∠PBA=∠C,
∴∠PBA+∠OBA=90°,即PB⊥OB.
∴PB是⊙O的切线.
(2)解:⊙O的半径为![]() ,∴OB=
,∴OB=![]() ,AC=
,AC=![]() .
.
∵OP∥BC,
∴∠BOP=∠OBC=∠C.
又∵∠ABC=∠PBO=90°,
∴△ABC∽△PBO,
∴![]() ,即
,即![]() .
.
∴BC=2.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:
【题目】在开展“好书伴我成长”的读书活动中,某中学为了解八年级300名学生读书情况,随机调查了八年级50名学生读书的册数.统计数据如下表所示:
册数 | 0 | 1 | 2 | 3 | 4 |
人数 | 3 | 13 | 16 | 17 | 1 |
(1)求这50个样本数据的平均救,众数和中位数.
(2)根据样本数据,估计该校八年级300名学生在本次活动中读书多于2册的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中不正确的有( )
①1是绝对值最小的数; ②0既不是正数,也不是负数;
③一个有理数不是整数就是分数; ④0的绝对值是0.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一组数据:5,15,75,45,25,75,45,35,45,35,那么40是这一组数据的( )
A. 平均数但不是中位数 B. 平均数也是中位数
C. 众数 D. 中位数但不是平均数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列计算正确的是( )
A. (x+y)2=x2+y2 B. (x﹣y)2=x2﹣2xy﹣y2
C. x(x﹣1)=x2﹣1 D. (x+1)(x﹣1)=x2﹣1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com