
如图,在正方形ABCD中,点M是BC边上的任一点,连接AM并将线段AM绕M顺时针旋转90°得到线段MN,在CD边上取点P使CP=BM,连接NP,BP.
(1)求证:四边形BMNP是平行四边形;
(2)线段MN与CD交于点Q,连接AQ,若△MCQ∽△AMQ,则BM与MC存在怎样的数量关系?请说明理由.
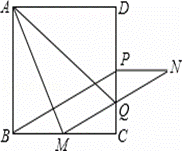
1)证明:在正方形ABCD中,AB=BC,∠ABC=∠B,
在△ABM和△BCP中,
 ,
,
∴△ABM≌△BCP(SAS),
∴AM=BP,∠BAM=∠CBP,
∵∠BAM+∠AMB=90°,
∴∠CBP+∠AMB=90°,
∴AM⊥BP,
∵AM并将线段AM绕M顺时针旋转90°得到线段MN,
∴AM⊥MN,且AM=MN,
∴MN∥BP,
∴四边形BMNP是平行四边形; --------4分
(2)解:BM=MC. -------1分
理由如下:∵∠BAM+∠AMB=90°,∠AMB+∠CMQ=90°,
∴∠BAM=∠CMQ,
又∵∠B=∠C=90°,
∴△ABM∽△MCQ,
∴ =
= ,
,
∵△MCQ∽△AMQ,
∴△AMQ∽△ABM,
∴ =
= ,
,
∴ =
= ,
,
∴BM=MC.


科目:初中数学 来源: 题型:
一辆慢车与一辆快车分别从甲、乙两地同时出发,匀速相向而行,两车在途中相遇后都停留一段时间,然后分别按原速一同驶往甲地后停车.设慢车行驶的时间为x小时,两车之间的距离为y千米,图中折线表示y与x之间的函数图象,请根据图象解决下列问题:
(1)甲乙两地之间的距离为 千米;
(2)求快车和慢车的速度;
(3)求线段DE所表示的y与x之间的函数关系式,并写出自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
为了预防“甲流”,某校对教室采用药熏消毒法进行消毒。已知药物燃烧时,室内每立方米空气中的含药量 y(mg)与时间x(min)成正比例,药物燃烧完后,y与x成反比例。现在测得药物8min燃毕,此时室内空气中每立方米含药量6mg,请根据题中所提供信息,解答下列问题:
(1)药物燃烧时,y关于x的函数关系式 ,
药物燃烧后, y关于x的函数关系式 ;
 (2)研究表明,每立方米的含药量不超过1.6mg时,学生方可进教室,那么从消毒开始,至少需要经过多少分钟后,学生才能回教室?
(2)研究表明,每立方米的含药量不超过1.6mg时,学生方可进教室,那么从消毒开始,至少需要经过多少分钟后,学生才能回教室?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com