
分析 (1)原式利用异号两数相加的法则计算即可得到结果;
(2)原式先计算绝对值运算,再计算减法运算即可;
(3)原式利用减法法则变形,计算即可得到结果;
(4)原式先计算乘方运算,再计算乘除运算,最后算加减运算即可得到结果.
解答 解:(1)(-20)+(+8)=-(20-8)=-12;
(2)-2-|-3|=-2-3=-5;
(3)(-4.9)+(+30)+(+4.9)-(-45)=-4.9+30+4.9+45=-4.9+4.9+30+45=75;
(4)-22÷(-2)2+(-3)2×(-$\frac{2}{3}$)=-1-6=-7.
点评 此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.


科目:初中数学 来源: 题型:解答题
 如图,在边长为4的正方形ABCD中,E是BC的中点,F是CD上一点,且CF=$\frac{1}{4}$CD.
如图,在边长为4的正方形ABCD中,E是BC的中点,F是CD上一点,且CF=$\frac{1}{4}$CD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
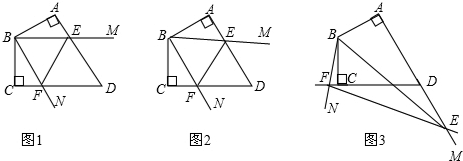
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
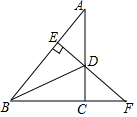 填空:把下面的推理过程补充完整,并在括号内注明理由.
填空:把下面的推理过程补充完整,并在括号内注明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 日期 | 10月1日 | 10月2日 | 10月3日 | 10月4日 | 10月5日 | 10月6日 | 10月7日 |
| 人数变化(万人) | +1.6 | +0.7 | +0.3 | -0.3 | -0.8 | +0.2 | -1.4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
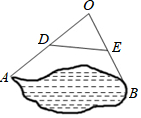 如图,为测量池塘边上两点A,B之间的距离,可以在池塘的一侧选取一点O,连接OA,OB,并分别取它们的中点D,E,连接DE,现测出AO=36米,BO=30米,DE=20米,那么A,B间的距离是( )
如图,为测量池塘边上两点A,B之间的距离,可以在池塘的一侧选取一点O,连接OA,OB,并分别取它们的中点D,E,连接DE,现测出AO=36米,BO=30米,DE=20米,那么A,B间的距离是( )| A. | 30米 | B. | 40米 | C. | 60米 | D. | 72米 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
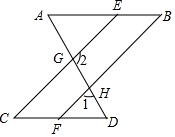 如图,已知∠A=∠AGE,∠D=∠DGC.
如图,已知∠A=∠AGE,∠D=∠DGC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com