
【题目】一名守门员练习沿直线折返跑,从球门线出发,向前记做正数,返回记做负数,他的记录如下(单位:m):+5,-3,+10,-8,-6,+12,-10.
(1)在这次往返跑中,守门员一共跑了多少米?
(2)请你借助数轴知识进行分析,回答守门员离开球门线最远是多少米?
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:
【题目】(2016湖北襄阳第25题)
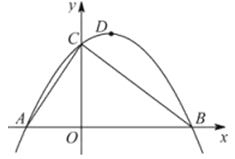
如图,已知点A的坐标为(-2,0),直线y=-![]() +3与x轴,y轴分别交于点B和点C,连接AC,顶点为D的抛物线y=ax2+bx+c过A,B,C三点.
+3与x轴,y轴分别交于点B和点C,连接AC,顶点为D的抛物线y=ax2+bx+c过A,B,C三点.
(1)请直接写出B,C两点的坐标,抛物线的解析式及顶点D的坐标;
(2)设抛物线的对称轴DE交线段BC于点E,P为第一象限内抛物线上一点,过点P作x轴的垂线,交线段BC于点F若四边形DEFP为平行四边形,求点P的坐标;
(3)设点M是线段BC上的一动点,过点M作MN∥AB,交AC于点N点.Q从点B出发,以每秒l个单位长度的速度沿线段BA向点A运动,运动时间为t(秒).当t(秒)为何值时,存在QMN为等腰直角三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,以点(2,3)为圆心、3为半径的圆,一定( )
A.与x轴相切,与y轴相切
B.与x轴相切,与y轴相交
C.与x轴相交,与y轴相切
D.与x轴相交,与y轴相交
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线m:y=ax2﹣6ax+c(a>0)的顶点A在x轴上,并过点B(0,1),直线n:y=﹣![]() x+
x+![]() 与x轴交于点D,与抛物线m的对称轴l交于点F,过B点的直线BE与直线n相交于点E(﹣7,7).
与x轴交于点D,与抛物线m的对称轴l交于点F,过B点的直线BE与直线n相交于点E(﹣7,7).
(1)求抛物线m的解析式;
(2)P是l上的一个动点,若以B,E,P为顶点的三角形的周长最小,求点P的坐标;
(3)抛物线m上是否存在一动点Q,使以线段FQ为直径的圆恰好经过点D?若存在,求点Q的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】长方形的一边长为2a+3b,另一边比它小a-b,那么这个长方形的周长是( )
A. 14a+6b B. 3a+7b C. 6a+14b D. 6a+10b
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题正确的是( )
A. 一组对边相等,另一组对边平行的四边形是平行四边形
B. 对角线相互垂直的四边形是菱形
C. 对角线相等的四边形是矩形
D. 对角线相互垂直平分且相等的四边形是正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】煤气费的收费标准为每月用气若不超过60m3,按每立方米0.8元收费;如果超过60m3,超过部分按每立方米1.2元收费.已知某住户某个月用煤气xm3(x>60),则该住户应交煤气费________元.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com