
【题目】如图⊙O的内接△ABC中,外角∠ACF的角平分线与⊙O相交于D点,DP⊥AC,垂足为P,DH⊥BF,垂足为H.问:
(1)∠PDC与∠HDC是否相等,为什么?
(2)图中有哪几组相等的线段?
(3)当△ABC满足什么条件时,△CPD∽△CBA,为什么?

【答案】(1)相等,理由详见解析;(2)PC=HC,DP=DH,AP=BH,AD=BD;(3)∠ABC=90°且∠ACB=60°时,△CPD∽△CBA.
【解析】
(1)根据“AAS”证明△CDH≌△CDP即可;
(2)发现全等三角形,根据全等三角形的对应边相等证明出线段相等;
(3)根据其中一个是直角三角形得到AC必须是直径.再根据另一对角对应相等,结合利用平角发现∠PCD=∠DCF=∠ACB=60°才可.
解 (1)相等.理由如下:
∵CD为∠ACF的角平分线(已知),
∴∠DCP=∠DCH,
∵DP⊥AC,DH⊥BF.
∴∠DPC=∠DHC=90°,
又∵CD=CD,
∴△CDH≌△CDP,
∴∠PDC=∠HDC.
(2) ∵△CDH≌△CDP,
∴PC=HC,DP=DH,
∵∠DAP=∠DBH,∠APD=∠BHD=90°,
∴△ADP≌△BDH,
∴AP=BH,AD=BD.
综上可得:PC=HC,DP=DH,AP=BH,AD=BD.
(3)∠ABC=90°且∠ACB=60°时,△CPD∽△CBA.
∵∠CPD=90°,
∴∠ABC=90°.
∵CD为∠ACF的角平分线,∠PCD=∠DCF=∠ACB,
∴∠ACB=60°.
∴∠ABC=90°且∠ACB=60°时,△CPD∽△CBA.


科目:初中数学 来源: 题型:
【题目】如图,科技小组准备用材料围建一个面积为60m2的矩形科技园ABCD,其中一边AB靠墙,墙长为12m。设AD的长为xm,DC的长为ym。
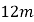
(1)求y与x之间的函数关系式;
(2)若围成矩形科技园ABCD的三边材料总长不超过26m,材料AD和DC的长都是整米数,求出满足条件的所有围建方案。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,一段街道的两边沿所在直线分别为AB,PQ,并且AB∥PQ,建筑物的一端DE所在的直线MN⊥AB于点M,交PQ于点N,小亮从胜利街的A处,沿着AB方向前进,小明一直站在点P的位置等待小亮.
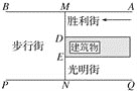
(1)请你画出小亮恰好能看见小明的视线,以及此时小亮所在的位置(用点C标出).
(2)已知:MN=30 m,MD=12 m,PN=36 m.求(1)中的点C到胜利街口的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,六边形ABCDEF∽六边形GHIJKL,相似比为2:1,则下列结论正确的是( )

A. ∠E=2∠K B. BC=2HI C. 六边形ABCDEF的周长=六边形GHIJKL的周长 D. S六边形ABCDEF=2S六边形GHIJKL
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一幅长20cm、宽12cm的图案,如图,其中有一横两竖的彩条,横、竖彩条的宽度比为3:2.设竖彩条的宽度为xcm,图案中三条彩条所占面积为ycm2.
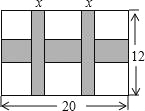
(1)求y与x之间的函数关系式;
(2)若图案中三条彩条所占面积是图案面积的![]() ,求横、竖彩条的宽度.
,求横、竖彩条的宽度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将正方形网格放置在平面直角坐标系中,其中每个小正方形的边长均为1,△ABC经过平移后得到△A1B1C1,若AC上一点P(1.2,1.4)平移后对应点为P1,点P1绕原点顺时针旋转180°,对应点为P2,则点P2的坐标为( )
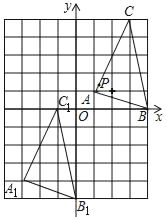
A. (2.8,3.6) B. (﹣2.8,﹣3.6)
C. (3.8,2.6) D. (﹣3.8,﹣2.6)
查看答案和解析>>
科目:初中数学 来源: 题型:
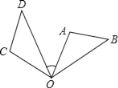
【题目】如图,将△OAB绕点O逆时针旋转80°得到△OCD,点A与点C是对应点.
(1)画出△OAB关于点O对称的图形(保留画图痕迹,不写画法);
(2)若∠A=110°,∠D=40°,求∠AOD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
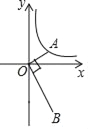
【题目】如图,已知点A是反比例函数y=![]() (x>0)的图象上的一个动点,连接OA,OB⊥OA,且OB=2OA,那么经过点B的反比例函数图象的表达式为( )
(x>0)的图象上的一个动点,连接OA,OB⊥OA,且OB=2OA,那么经过点B的反比例函数图象的表达式为( )
A. y=﹣![]() B. y=
B. y=![]() C. y=﹣
C. y=﹣![]() D. y=
D. y=![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
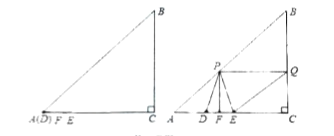
【题目】如图,在Rt△ABC中,∠C=90°,AC=BC=10cm,长为4cm的线段DE在边AC上,且点D与点A重合,点F是DE的中点,线段DE从点A出发,沿AC方向向点C匀速运动,直到点E与点C重合,速度1cm/s。过点F作PF⊥AC,交AB于点P,过点P作PQ//AC,交BC于点Q,连接PD,PE,QE,设线段DE的运动时间为t(s).(0≤t≤6)
(1)请分别用含有t的代数式表示线段PF、BQ
(2)当t为何值时,四边形PFCQ为正方形?
(3)设四边形PDEQ的面积为y(cm)请求出y与t之间的函数关系式,并求出当t为何值时,四边形PDEQ的面积最大,最大是多少?
(4)是否存在某一时刻t,使得EP平分∠AEQ?若存在,求出此时t的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com