
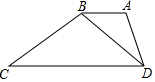
 在梯形ABCD中,AB∥CD,连结BD,且∠ADB=∠C,又AB=8,BC=15,AD=10,求CD的长.
在梯形ABCD中,AB∥CD,连结BD,且∠ADB=∠C,又AB=8,BC=15,AD=10,求CD的长. 分析 由AB∥CD知∠ABD=∠BDC,结合∠ADB=∠C可证△ABD∽△BDC,得$\frac{AB}{BD}=\frac{AD}{BC}=\frac{BD}{DC}$,据此可得.
解答 解:∵AB∥CD,
∴∠ABD=∠BDC,
又∵∠ADB=∠C,
∴△ABD∽△BDC,
则$\frac{AB}{BD}=\frac{AD}{BC}=\frac{BD}{DC}$,即$\frac{8}{BD}=\frac{10}{15}=\frac{BD}{DC}$,
解得:BD=12,CD=18.
点评 本题主要考查相似三角形的判定与性质及平行线的性质,在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用,寻找相似三角形的一般方法是通过作平行线构造相似三角形;或依据基本图形对图形进行分解、组合;或作辅助线构造相似三角形,判定三角形相似的方法有事可单独使用,有时需要综合运用,无论是单独使用还是综合运用,都要具备应有的条件方可.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
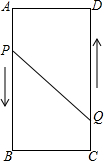 A、B、C、D为矩形的四个顶点,AB=16cm,AD=6cm,动点P、Q分别从点A、C同时出发,点P以3cm/s的速度向点B移动,一直到达B为止,点Q以2cm/s的速度向D移动.
A、B、C、D为矩形的四个顶点,AB=16cm,AD=6cm,动点P、Q分别从点A、C同时出发,点P以3cm/s的速度向点B移动,一直到达B为止,点Q以2cm/s的速度向D移动.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
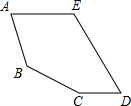 聪聪用五根宽度相同的木条拼成了一个五边形,如图所示,已知AE∥CD,∠A=$\frac{1}{2}$∠C,∠B=120°,∠D=50°.
聪聪用五根宽度相同的木条拼成了一个五边形,如图所示,已知AE∥CD,∠A=$\frac{1}{2}$∠C,∠B=120°,∠D=50°.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,将△ABC沿着过AB中点D的直线折叠,使点A落在BC边上的A1处,称为第1次操作,折痕DE到BC的距离记为h1,还原纸片后,再将△ADE沿着过AD中点D1的直线折叠,使点A落在DE边上的A2处,称为第2次操作,折痕D1E1到BC的距离记为h2;按上述方法不断操作下去…,经过第2015次操作后得到的折痕D2014E2014,到BC的距离记为h2015;若h1=1,则h2016的值为2-$\frac{1}{{2}^{2015}}$.
如图,将△ABC沿着过AB中点D的直线折叠,使点A落在BC边上的A1处,称为第1次操作,折痕DE到BC的距离记为h1,还原纸片后,再将△ADE沿着过AD中点D1的直线折叠,使点A落在DE边上的A2处,称为第2次操作,折痕D1E1到BC的距离记为h2;按上述方法不断操作下去…,经过第2015次操作后得到的折痕D2014E2014,到BC的距离记为h2015;若h1=1,则h2016的值为2-$\frac{1}{{2}^{2015}}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com