【题目】如图 ，△ABC是等腰直角三角形，∠A=90ｏ，点P、Q分别是AB、AC上的动点，且满足BP=AQ，D是BC的中点。
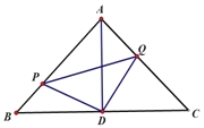
（1）求证：△PDQ是等腰直角三角形；
（2）当点P运动到什么位置时，四边形ＡPDQ是正方形，说明理由。
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】已知如图，∠COD=90°，直线AB与OC交于点B，与OD交于点A，射线OE和射线AF交于点G．
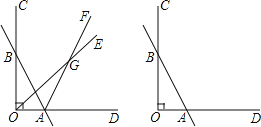
（1）若OE平分∠BOA，AF平分∠BAD，∠OBA=30°，则∠OGA=
（2）若∠GOA=
∠BOA，∠GAD=∠BAD，∠OBA=30°，则∠OGA=
（3）将（2）中“∠OBA=30°”改为“∠OBA=α”，其余条件不变，则∠OGA= α （用含α的代数式表示）
（4）若OE将∠BOA分成1：2两部分，AF平分∠BAD，∠ABO=α（30°＜α＜90°），求∠OGA的度数（用含α的代数式表示）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，在四边形ABCD的边AB上任取一点E（点E不与点A、点B重合），分别连接ED，EC，可以把四边形ABCD分成三个三角形，如果其中有两个三角形相似，我们就把E叫做四边形ABCD的边AB上的相似点；如果这三个三角形都相似，我们就把E叫做四边形ABCD的边AB上的强相似点．解决问题：
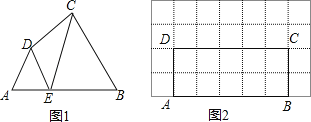
（1）如图1，∠A=∠B=∠DEC=55°，试判断点E是否是四边形ABCD的边AB上的相似点，并说明理由；
（2）如图2，在矩形ABCD中，AB=5，BC=2，且A，B，C，D四点均在正方形网格（网格中每个小正方形的边长为1）的格点（即每个小正方形的顶点）上，试在图2中画出矩形ABCD的边AB上的一个强相似点E．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】等腰Rt△ABC中，∠BAC＝90°，AB＝AC,点A、点B分别是y轴、x轴上两个动点，直角边AC交x轴于点D，斜边BC交y轴于点E；
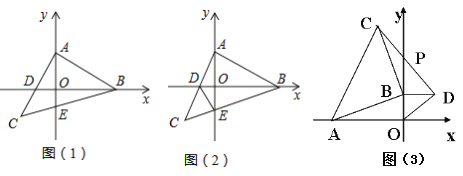
（1）如图（1），已知C点的横坐标为-1，直接写出点A的坐标；
（2）如图（2）， 当等腰Rt△ABC运动到使点D恰为AC中点时，连接DE，求证：∠ADB＝∠CDE；
（3）如图（3）， 若点A在x轴上，且A（-4，0），点B在y轴的正半轴上运动时，分别以OB、AB为直角边在第一、二象限作等腰直角△BOD和等腰直角△ABC，连结CD交y轴于点P,问当点B在y轴的正半轴上运动时，BP的长度是否变化？若变化请说明理由，若不变化，请求出BP的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
