
 如图,已知直线l1:y=-$\sqrt{3}$x+$\sqrt{3}$与x轴y轴分别交于A,B两点,C(2,2$\sqrt{3}$).
如图,已知直线l1:y=-$\sqrt{3}$x+$\sqrt{3}$与x轴y轴分别交于A,B两点,C(2,2$\sqrt{3}$).分析 (1)在y=-$\sqrt{3}$x+$\sqrt{3}$中,令x=0,则y=$\sqrt{3}$,令y=0,则x=1,于是得到距离;
(2)如图1,过C作CD⊥x轴于D,根据C(2,2$\sqrt{3}$),于是得到OD=2,CD=2$\sqrt{3}$,即可求得S△ABC=S梯形BODC-S△ABO-S△ACD=$\frac{1}{2}$($\sqrt{3}+2\sqrt{3}$)×2-$\frac{1}{2}×1×\sqrt{3}$-$\frac{1}{2}×1×2\sqrt{3}$=$\frac{3\sqrt{3}}{2}$;
(3)如图2所示,根据S△PBA=S△ABC,于是得到所有满足条件的P点所构成的图象是一条平行于AB且到AB的距离等于点C到AB的距离的直线,设这条直线的解析式为y=-$\sqrt{3}$x+b,根据点到直线的距离公式得到C到直线AB的距离为:$\frac{|\sqrt{3}×2+1×2\sqrt{3}-\sqrt{3}|}{\sqrt{(\sqrt{3})^{2}+{1}^{2}}}$=$\frac{3\sqrt{3}}{2}$,根据点A到直线y=-$\sqrt{3}$x+b的距离=C到直线AB的距离,求出b=-4$\sqrt{3}$,即可求得结论.
解答 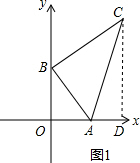 解:(1)在y=-$\sqrt{3}$x+$\sqrt{3}$中,
解:(1)在y=-$\sqrt{3}$x+$\sqrt{3}$中,
令x=0,则y=$\sqrt{3}$,令y=0,则x=1,
∴A(1,0),B(0,$\sqrt{3}$),
(2)如图1,过C作CD⊥x轴于D,
∵C(2,2$\sqrt{3}$),
∴OD=2,CD=2$\sqrt{3}$,
∴S△ABC=S梯形BODC-S△ABO-S△ACD=$\frac{1}{2}$($\sqrt{3}+2\sqrt{3}$)×2-$\frac{1}{2}×1×\sqrt{3}$-$\frac{1}{2}×1×2\sqrt{3}$=$\frac{3\sqrt{3}}{2}$;
(3)如图2所示,
∵S△PBA=S△ABC,
∴所有满足条件的P点所构成的图象是一条平行于AB且到AB的距离等于点C到AB的距离的直线,
设这条直线的解析式为y=-$\sqrt{3}$x+b,
∵C到直线AB的距离为:$\frac{|\sqrt{3}×2+1×2\sqrt{3}-\sqrt{3}|}{\sqrt{(\sqrt{3})^{2}+{1}^{2}}}$=$\frac{3\sqrt{3}}{2}$,
∴点A到直线y=-$\sqrt{3}$x+b的距离=C到直线AB的距离,
∴$\frac{|\sqrt{3}×1+b|}{\sqrt{(\sqrt{3})^{2}+1}}$=$\frac{3\sqrt{3}}{2}$,
∵b<0,
∴b=-4$\sqrt{3}$,
∴该图象的函数关系式为:y=-$\sqrt{3}$x-4$\sqrt{3}$.
点评 本题考查了一次函数的性质,求一次函数的解析式,三角形的面积的计算,根据函数的解析式求点的坐标,点到直线的距离公式,根据题目所给信息得到所有满足条件的P点所构成的图象是一条直线是解题的关键.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案科目:初中数学 来源: 题型:解答题
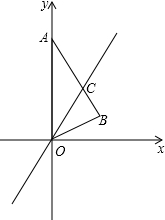 如图,在平面直角坐标系中,Rt△ABO的斜边OA落在y轴的正半轴上,OA、OB的长是方x2-6x+8=0的两根,把△AOB折叠,使点B落在y轴正半轴上,折痕与AB边相交于点C.
如图,在平面直角坐标系中,Rt△ABO的斜边OA落在y轴的正半轴上,OA、OB的长是方x2-6x+8=0的两根,把△AOB折叠,使点B落在y轴正半轴上,折痕与AB边相交于点C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
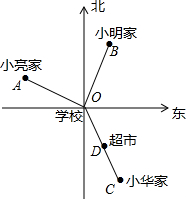 如图,点A,B,C,D,O分别表示小亮家、小明家、小华家、超市、学校的位置.点A位于点O北偏西65°,点B位于点O北偏东25°,点C位于点O南偏东30°,且点D是线段OC的中点.
如图,点A,B,C,D,O分别表示小亮家、小明家、小华家、超市、学校的位置.点A位于点O北偏西65°,点B位于点O北偏东25°,点C位于点O南偏东30°,且点D是线段OC的中点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
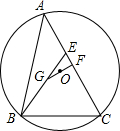 如图,⊙O是△ABC的外接圆,E为AC上一点,且△EBC是等边△,OF⊥AC于F,FO的延长线交BE于G,AE=3,EG=2,求AB的长.
如图,⊙O是△ABC的外接圆,E为AC上一点,且△EBC是等边△,OF⊥AC于F,FO的延长线交BE于G,AE=3,EG=2,求AB的长.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com