Question

顺次连接矩形各边中点所得的四边形是________；顺次连接对角线互相垂直的四边形各边中点所得的四边形是________．

Answer 1

菱形    矩形
分析：结合图形，运用中位线定理及特殊四边形的判定判断．根据三角形中位线的性质，可得到这个四边形是平行四边形，再由对角线垂直，能证出有一个角等于90°，则这个四边形为矩形．
解答：

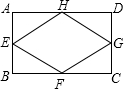
∵矩形的对角线相等，
∴顺次连接矩形四条边的中点，所围成的四边形是菱形；

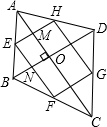
∵E、F、G、H分别为各边的中点，
∴EF∥AC，GH∥AC，EH∥BD，FG∥BD，（三角形的中位线平行于第三边）
∴四边形EFGH是平行四边形，（两组对边分别平行的四边形是平行四边形）
∵AC⊥BD，EF∥AC，EH∥BD，
∴∠EMO=∠ENO=90°，
∴四边形EMON是矩形（有三个角是直角的四边形是矩形），
∴∠MEN=90°，
∴四边形EFGH是矩形（有一个角是直角的平行四边形是矩形）．
故答案为：菱形；矩形．
点评：主要考查了三角形中位线定理中的数量关系：中位线等于所对应的边长的一半．解题的关键是根据中位线定理得出所求的四边形边的数量关系和位置关系，再根据对角线的数量关系和位置关系进行判断．