
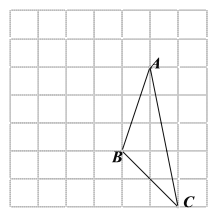
【题目】画图(只能借助于网格)并填空:
如图,每个小正方形的边长为![]() 个单位,每个小正方形的顶点叫格点.
个单位,每个小正方形的顶点叫格点.
(1)将![]() 向左平移
向左平移![]() 格,再向上平移
格,再向上平移![]() 格,请在图中画出平移后的
格,请在图中画出平移后的![]() ;
;
(2)![]() 的面积为 ;
的面积为 ;
(3)利用网格在图中画出△ABC的中线![]() ,高线
,高线![]() ;
;
(4)在图中能使![]() 的格点
的格点![]() 的个数有 个(点
的个数有 个(点![]() 异于
异于![]() ).
).
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:
【题目】阅读材料: 小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如:![]() ,善于思考的小明进行了以下探索:
,善于思考的小明进行了以下探索:
设![]() (其中
(其中![]() 均为整数),则有
均为整数),则有![]() .
.
∴![]() .这样小明就找到了一种把部分
.这样小明就找到了一种把部分![]() 的式子化为平方式的方法.
的式子化为平方式的方法.
请你仿照小明的方法探索并解决下列问题:
当![]() 均为正整数时,若
均为正整数时,若![]() ,用含m、n的式子分别表示
,用含m、n的式子分别表示![]() ,得
,得![]() = ,
= ,![]() = ;
= ;
(2)利用所探索的结论,找一组正整数![]() ,填空: + =( +
,填空: + =( + ![]() )2;
)2;
(3)若![]() ,且
,且![]() 均为正整数,求
均为正整数,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC是等边三角形,D是AB边上任意一点,∠CDE=60°,DE与∠ABC外角平分线相交于点E.
(1)求证:CD=DE;

(2)若D是AB延长线上任意一点,∠CDE=60°,DE与∠ABC外角平分线相交于点E.请画出图形,判断CD=DE是否还成立?若成立,请给予证明;若不成立,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BE是线段AB的延长线,且∠CBE=∠A=∠C.
(1)由∠CBE=∠A可以判断____∥_____,根据是_____________;
(2)由∠CBE=∠C可以判断____∥_____,根据是_____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(探究发现)
如图1,在△ABC中,点P是内角∠ABC和外角∠ACD的角平分线的交点,试猜想∠P与∠A之间的数量关系,并证明你的猜想.

(迁移拓展)
如图2,在△ABC中,点P是内角∠ABC和外角∠ACD的n等分线的交点,即∠PBC=![]() ∠ABC,∠PCD=
∠ABC,∠PCD=![]() ∠ACD,
∠ACD,
试猜想∠P与∠A之间的数量关系,并证明你的猜想.
(应用创新)
已知,如图3,AD、BE相交于点C,∠ABC、∠CDE、∠ACE的角平分线交于点P,∠A=35°,∠E=25°,则∠BPD= .
查看答案和解析>>
科目:初中数学 来源: 题型:
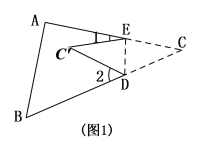
【题目】如图1,将△ABC纸片沿DE折叠,使点C落在四边形ABDE内点C’的位置,
(1)①若![]() ,则
,则![]() ;
;
②若![]() ,则
,则![]() ;
;
③探索![]() 、
、![]() 与
与![]() 之间的数量关系,并说明理由;
之间的数量关系,并说明理由;
(2)直接按照所得结论,填空:
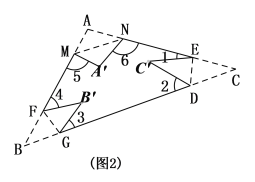
①如图中,将△ABC纸片再沿FG、MN折叠,使点A、B分别落在△ABC内点A’、B’的位置,则![]() ;
;
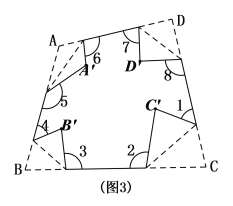
②如图中,将四边形ABCD按照上面方式折叠,则![]() ;
;
③若将n边形![]() 也按照上面方式折叠,则
也按照上面方式折叠,则![]() ;
;
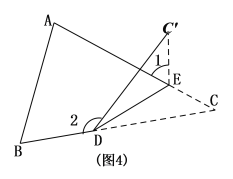
(3)如图,将△ABC纸片沿DE折叠,使点![]() 落在△ABC边
落在△ABC边![]() 上方点
上方点![]() 的位置, 探索
的位置, 探索![]() 、
、![]() 与
与![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
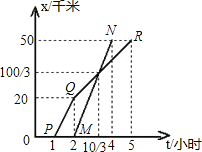
【题目】如图,AB两地相距50千米,甲于某日下午1时骑自行车从A地出发驶往B地,乙也于同日下午骑摩托车从A地出发驶往B地,图中PQR和线段MN,分别表示甲和乙所行驶的S与该日下午时间t之间的关系,试根据图形回答:
(1)甲出发几小时,乙才开始出发?
(2)乙行驶多少分钟赶上甲,这时两人离B地还有多少千米?
(3)甲从下午2时到5时的速度是多少?
(4)乙行驶的速度是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD中,AE平分∠BAD,交BC于E,DE⊥AE,下列结论::①DE平分∠ADC;②E是BC的中点;③AD=2CD;④梯形ADCE的面积与△ABE的面积比是3:1,其中正确的结论的个数有( )
A.4
B.3
C.2
D.1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com