
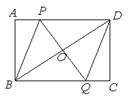
如图,在矩形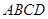 中,点
中,点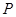 是线段
是线段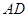 上一动点,
上一动点,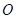 为
为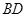 的中点,
的中点,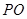 的延长线交
的延长线交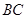 于
于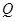 .
.
(1)求证: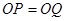 ;(4分)
;(4分)
(2)若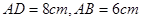 ,
,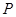 从点
从点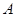 出发,以1cm/s的速度向
出发,以1cm/s的速度向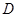 运动(不与
运动(不与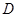 重合).设点
重合).设点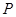 运动时间为
运动时间为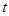 秒,请用
秒,请用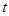 表示
表示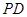 的长;并求
的长;并求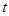 为何值时,四边形
为何值时,四边形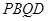 是菱形.(6分)
是菱形.(6分)
(1)通过对菱形的证明从而求证(2)
【解析】
试题分析:(1)证明:∵四边形ABCD是矩形
∴AD∥BC,
∴∠PDO=∠QBO
又∵OB=OD,∠POD=∠QOB
∴△POD≌△QOB
∴OP=OQ 4分
(2)①PD=8-t 6分
②若四边形PBQD是菱形,则PB=PD=(8-t)cm, 7分
∵四边形ABCD是矩形
∴∠A=90°
∴在Rt△ABP中,∵AB="6cm"
∴
∴
∴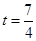 ,
9分
,
9分
即运动时间为 秒时,四边形PBQD是菱形.
秒时,四边形PBQD是菱形.
考点:二次函数的综合题
点评:在解题时要能灵运用二次函数的图象和性质求出二次函数的解析式,利用数形结合思想解题是本题的关键.,


科目:初中数学 来源: 题型:
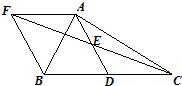 24、如图,在△ABC中,D是BC的中点,E是AD的中点,过点A作AF∥BC,AF与CE的延长线相交于点F,连接BF.
24、如图,在△ABC中,D是BC的中点,E是AD的中点,过点A作AF∥BC,AF与CE的延长线相交于点F,连接BF.查看答案和解析>>
科目:初中数学 来源: 题型:
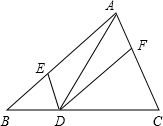 如图,在△ABC中,点E、D、F分别在边AB、BC、CA上,且DE∥CA,DF∥BA.
如图,在△ABC中,点E、D、F分别在边AB、BC、CA上,且DE∥CA,DF∥BA.查看答案和解析>>
科目:初中数学 来源: 题型:
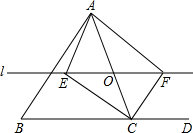 如图,在△ABC中,O是AC上的任意一点,(不与点A,C重合),过点O作直线l∥BC,直线l与∠BCA的平分线相交于点E,与∠DCA的平分线相交于点F.
如图,在△ABC中,O是AC上的任意一点,(不与点A,C重合),过点O作直线l∥BC,直线l与∠BCA的平分线相交于点E,与∠DCA的平分线相交于点F.查看答案和解析>>
科目:初中数学 来源:2012-2013学年陕西省西安市庆安中学八年级上学期期中考试数学试卷(带解析) 题型:解答题
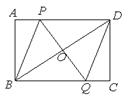
如图,在矩形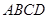 中,点
中,点 是线段
是线段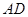 上一动点,
上一动点,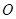 为
为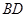 的中点,
的中点,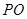 的延长线交
的延长线交 于
于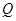 .
.
(1)求证: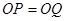 ;(4分)
;(4分)
(2)若 ,
, 从点
从点 出发,以1cm/s的速度向
出发,以1cm/s的速度向 运动(不与
运动(不与 重合).设点
重合).设点 运动时间为
运动时间为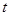 秒,请用
秒,请用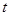 表示
表示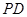 的长;并求
的长;并求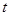 为何值时,四边形
为何值时,四边形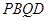 是菱形.(6分)
是菱形.(6分)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com