
【题目】如图,在平面直角坐标系xOy中,点B(-1,4),点A(-7,0),点P是直线![]() 上一点,且∠ABP=45°,则点P的坐标为____.
上一点,且∠ABP=45°,则点P的坐标为____.

【答案】(-![]() ,-
,-![]() )
)
【解析】
过点A作AH⊥BA,交BP于H,过点A作x轴的垂线,作BM⊥AM,HN⊥AN,求出直线BH的解析式,然后与![]() 联立方程组,求解即可.
联立方程组,求解即可.
过点A作AH⊥BA,交BP于H,过点A作x轴的垂线,作BM⊥AM,HN⊥AN,

∵∠ABP=45°
∴AB=AH
∵根据直角三角形性质得:∠AMB=∠ANH, ∠MBA=∠NAH,
∴△BMA≌△ANH,
∴AN=BM=-1-(-7)=6,NH=AM=4 ,
∴H的横坐标是:-7+4=-3
∴H(-3,-6),
设直线BH为y=kx+b
把H(-3,-6), B(-1,4)代入得
![]()
解得![]()
∴直线BH为:y=5x+9
∴y=5x+9与![]() 联立方程组为
联立方程组为
![]() ,
,
解得: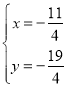 ,即P(-
,即P(-![]() ,-
,-![]() ).
).


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y=mx+n的图像与x轴交于点B,与反比例函数![]() (k﹥0)的图像交于点C,过点C作CH⊥x轴,点D是反比例函数图像上的一点,直线CD与x轴交于点A,若∠HCB=∠HCA,且BC=10,BA=16.
(k﹥0)的图像交于点C,过点C作CH⊥x轴,点D是反比例函数图像上的一点,直线CD与x轴交于点A,若∠HCB=∠HCA,且BC=10,BA=16.
(1)若OA=11,求k的值;
(2)沿着x轴向右平移直线BC,若直线经过H点时恰好又经过点D,求一次函数函数y=mx+n的表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
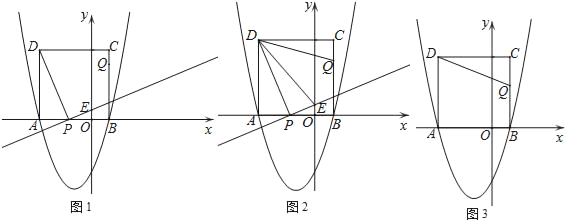
【题目】如图,二次函数y=x2+2x+c的图象与x轴交于点A和点B(1,0),以AB为边在x轴上方作正方形ABCD,动点P从点A出发,以每秒2个单位长度的速度沿x轴的正方向匀速运动,同时动点Q从点C出发,以每秒1个单位长度的速度沿CB匀速运动,当点Q到达终点B时,点P停止运动,设运动时间为t秒.连接DP,过点P作DP的垂线与y轴交于点E.
(1)求二次函数的解析式及点A的坐标;
(2)当点P在线段AO(点P不与A、O重合)上运动至何处时,线段OE的长有最大值,并求出这个最大值;
(3)在P,Q运动过程中,求当△DPE与以D,C,Q为顶点的三角形相似时t的值;
(4)是否存在t,使△DCQ沿DQ翻折得到△DC′Q,点C′恰好落在抛物线的对称轴上?若存在,请求出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中直线![]() :
:![]() 分别与x轴,y轴交于点A和点B,过点A的直线
分别与x轴,y轴交于点A和点B,过点A的直线![]() 与y轴交于点C,
与y轴交于点C,![]() .
.

(1)求直线![]() 的解析式;
的解析式;
(2)若D为线段![]() 上一点,E为线段
上一点,E为线段![]() 上一点,当
上一点,当![]() 时,求
时,求![]() 的最小值,并求出此时点E的坐标.
的最小值,并求出此时点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
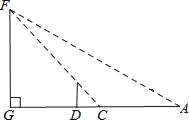
【题目】小明是个爱动脑筋的学生,在学习了解直角三角形以后,一天他去测量学校的旗杆GF的高度,此时过旗杆的顶点F的阳光刚好过身高DE为1.6米的小明的头顶且在他身后形成的影长DC=2米.
(1)若旗杆的高度FG是a米,用含a的代数式表示DG.
(2)小明从点C后退6米在A的测得旗杆顶点F的仰角为30°,求旗杆FG的高度.(点A、C、D、G在一条直线上, ![]() ,
, ![]() ,结果精确到0.1)
,结果精确到0.1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(a),直线l1:y=kx+b经过点A、B,OA=OB=3,直线12:y=![]() x﹣2交y轴于点C,且与直线l1交于点D,连接OD.
x﹣2交y轴于点C,且与直线l1交于点D,连接OD.

(1)求直线11的表达式;
(2)求△OCD的面积;
(3)如图(b),点P是直线11上的一动点;连接CP交线段OD于点E,当△COE与△DEP的面积相等时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了加强对校内外的安全监控,创建平安校园,某学校计划增加![]() 台监控摄像设备,现有甲、乙两种型号的设备,其中每台价格、有效监控半径如表所示,经调查,购买
台监控摄像设备,现有甲、乙两种型号的设备,其中每台价格、有效监控半径如表所示,经调查,购买![]() 台甲型设备比购买
台甲型设备比购买![]() 台乙型设备少
台乙型设备少![]() 元,购买
元,购买![]() 台甲型设备比购买
台甲型设备比购买![]() 台乙型设备多
台乙型设备多![]() 元.
元.
甲型 | 乙型 | |
价格(元/台) |
|
|
有效半径(米/台) |
|
|
(![]() )求
)求![]() ,
,![]() 的值;
的值;
(![]() )若购买该批设备的资金不超过
)若购买该批设备的资金不超过![]() 元,且两种型号的设备均要至少买一台,学校有哪几种购买方案?
元,且两种型号的设备均要至少买一台,学校有哪几种购买方案?
(![]() )在(
)在(![]() )的条件下,若要求监控半径覆盖范围不低于
)的条件下,若要求监控半径覆盖范围不低于![]() 米,为了节约资金,请你设计一种最省钱的购买方案.
米,为了节约资金,请你设计一种最省钱的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级八个班共有280名学生,男女生人数大致相同,调查小组为调查学生的体质健康水平,开展了一次调查研究,请将下面的过程补全.
收集数据:
(1)调查小组计划选取40名学生的体质健康测试成绩作为样本,下面的取样方法中,合理的是___________(填字母);
A.抽取九年级1班、2班各20名学生的体质健康测试成绩组成样本
B.抽取各班体育成绩较好的学生共40名学生的体质健康测试成绩组成样本
C.从年级中按学号随机选取男女生各20名学生学生的体质健康测试成绩组成样本
整理、描述数据:
抽样方法确定后,调查小组获得了40名学生的体质健康测试成绩如下:
77 83 80 64 86 90 75 92 83 81
85 86 88 62 65 86 97 96 82 73
86 84 89 86 92 73 57 77 87 82
91 81 86 71 53 72 90 76 68 78
整理数据,如下表所示:
2018年九年级部分学生学生的体质健康测试成绩统计表
|
|
|
|
|
|
|
|
|
|
1 | 1 | 2 | 2 | 4 | 5 | 5 | 2 |
分析数据、得出结论
调查小组将统计后的数据与去年同期九年级的学生的体质健康测试成绩(直方图)进行了对比,

(2)你能从中得到的结论是_____________,你的理由是________________________________.
(3)体育老师计划根据2018年的统计数据安排75分以下的同学参加体质加强训练项目,则全年级约有________名同学参加此项目.
查看答案和解析>>
科目:初中数学 来源: 题型:
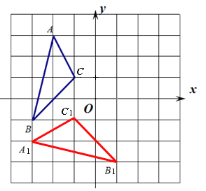
【题目】如图,已知△ABC三个顶点的坐标分别是A(-2,3),B(-3,-1),C(-1,1)
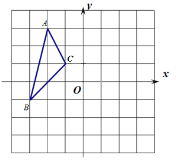
(1)画出△ABC绕点O逆时针旋转90°后的△A1B1C1,并写出点A1的坐标;
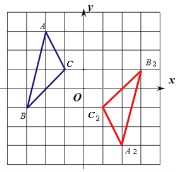
(2)画出△ABC绕点O逆时针旋转180°后的△A2B2C2,并写出点A2的坐标;
(3)直接回答:∠AOB与∠A2OB2有什么关系?
【答案】(1)作图见解析,(-4,-2);(2)作图见解析,(2,-3);(3)相等.
【解析】
试题分析:(1)根据旋转的性质作图,写出点的坐标;
根据旋转的性质作图,写出点的坐标;
(3)根据旋转的性质得出结论.
试题解析:(1)作图如下,点A1的坐标(-4,-2).
(2)作图如下,点A2的坐标(2,-3).
(3)相等.
考点:1.旋转作图;2.旋转的性质.
【题型】解答题
【结束】
20
【题目】已知函数y=(m﹣2)xm2+m-4 +2x﹣1是一个二次函数,求该二次函数的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com