
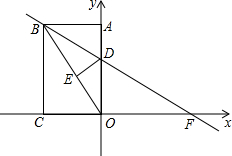
 如图,矩形ABCO中,点C在x轴上,点A在y轴上,点B的坐标是(-6,8).矩形ABCO沿直线BD折叠,使得点A落在对角线OB上的点E处,折痕与OA、x轴分别交于点D、F.
如图,矩形ABCO中,点C在x轴上,点A在y轴上,点B的坐标是(-6,8).矩形ABCO沿直线BD折叠,使得点A落在对角线OB上的点E处,折痕与OA、x轴分别交于点D、F.分析 (1)由矩形的性质得出∠BAD=∠OCB=90°,AB=OC=6,OA=BC=8,由勾股定理即可得出答案;
(2)由折叠的性质得:BE=AB=6,∠BED=∠BAD=90°,DE=AD,求出OE=BO-BE=4,∠OED=90°,设D(0,a),则OD=a,DE=AD=OA-OD=8-a,在Rt△EOD中,由勾股定理得出方程,解方程即可;
(3)①当OM、OE都为菱形的边时,OM=OE=4,得出M的坐标为(4,0)或(-4,0);
②当OM为菱形的边,OE为对角线时,MN垂直平分OE,垂足为G,则OG=$\frac{1}{2}$OE=2,由三角函数求出OM即可;
③当OM为菱形的对角线,OE为边时,同②得:M(-$\frac{24}{5}$,0);即可得出结论.
解答 解:(1)∵四边形ABCO是矩形,点B的坐标是(-6,8).
∴∠BAD=∠OCB=90°,AB=OC=6,OA=BC=8,
∴BO=$\sqrt{O{C}^{2}+B{C}^{2}}$=10;
(2)由折叠的性质得:BE=AB=6,∠BED=∠BAD=90°,DE=AD,
∴OE=BO-BE=10-6=4,∠OED=90°,
设D(0,a),则OD=a,DE=AD=OA-OD=8-a,
在Rt△EOD中,由勾股定理得:DE2+OE2=OD2,
即(8-a)2+42=a2,解得:a=5,
∴D(0,5);
(3)存在,点M的坐标为(4,0)或(-4,0)或(-$\frac{10}{3}$,0)或(-$\frac{24}{5}$,0);理由如下:
①当OM、OE都为菱形的边时,OM=OE=4,
∴M的坐标为(4,0)或(-4,0);
②当OM为菱形的边,OE为对角线时,MN垂直平分OE,垂足为G,如图1所示:
则OG=$\frac{1}{2}$OE=2,
则cos∠MOG=cos∠BOC,
∴$\frac{OG}{OM}=\frac{OC}{OB}$,即$\frac{2}{OM}=\frac{6}{10}$,
解得:OM=$\frac{10}{3}$,
∴M(-$\frac{10}{3}$,0);
③当OM为菱形的对角线,OE为边时,如图2所示:
同②得:M(-$\frac{24}{5}$,0);
综上所述,在x轴上存在点M,使以M、N、E、O为顶点的四边形是菱形,点M的坐标为(4,0)或(-4,0)或(-$\frac{10}{3}$,0)或(-$\frac{24}{5}$,0).
点评 本题是四边形综合题目,考查了矩形的性质,轴对称的性质,勾股定理,坐标与图形性质,三角函数,菱形的性质等知识;本题综合性强,有一定难度.


科目:初中数学 来源: 题型:选择题
| A. | $\frac{5}{6}$ | B. | $\frac{6}{11}$ | C. | $\frac{5}{11}$ | D. | $\frac{6}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5,3 | B. | 5,4 | C. | 7,3 | D. | 7,5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,△ABC在直角坐标系中的位置如图所示,点A的坐标为(1,2),若将△ABC绕点O旋转,点C的对应点为点D,则旋转后点A的对应点的坐标为( )
如图,△ABC在直角坐标系中的位置如图所示,点A的坐标为(1,2),若将△ABC绕点O旋转,点C的对应点为点D,则旋转后点A的对应点的坐标为( )| A. | (-1,2) | B. | (0,-1) | C. | (1,-3) | D. | (2,-1) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
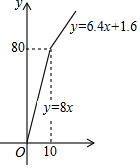 某书定价8元,如果一次购买10本以上,超过10本部分打八折,那么付款金额y与购书数量x之间的函数关系如何,同学们对此展开了讨论:
某书定价8元,如果一次购买10本以上,超过10本部分打八折,那么付款金额y与购书数量x之间的函数关系如何,同学们对此展开了讨论:| 购买量/本 | 1 | 2 | 3 | 4 | … | 9 | 10 | 11 | 12 | … |
| 付款金额/元 | 8 | 16 | 24 | 32 | … | 72 | 80 | 86.4 | 92.8 | … |
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com