
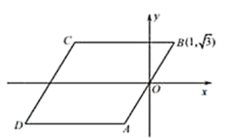
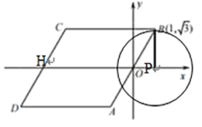
【题目】如图,已知四边形ABCD是菱形,BC∥x轴,点B的坐标是(1,![]() ),坐标原点O是AB的中点.动圆⊙P的半径是
),坐标原点O是AB的中点.动圆⊙P的半径是![]() ,圆心在x轴上移动,若⊙P在运动过程中只与菱形ABCD的一边相切,则点P的横坐标m 的取值范围是_________.
,圆心在x轴上移动,若⊙P在运动过程中只与菱形ABCD的一边相切,则点P的横坐标m 的取值范围是_________.
【答案】![]() 或
或![]() 或
或![]() 或
或![]()
【解析】
若⊙P在运动过程中只与菱形ABCD的一边相切,则需要对此过程分四种情况讨论,根据已知条件计算出m的取值范围即可.
解:由B点坐标(1,![]() ),及原点O是AB的中点可知AB=2,直线AB与x轴的夹角为60°,
),及原点O是AB的中点可知AB=2,直线AB与x轴的夹角为60°,
又∵四边形ABCD是菱形,
∴AD=AB=BC=CD=2,
设DC与x轴相交于点H,则OH=4,
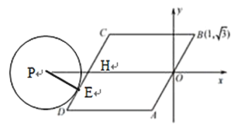
(1)当⊙P与DC边相切于点E时,连接PE,如图所示,
由题意可知PE=![]() ,PE⊥DC,∠PHE=60°,
,PE⊥DC,∠PHE=60°,
∴PH=2,
∴此时点P坐标为(-6,0),所以此时![]() .
.
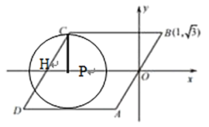
(2)当⊙P只与AD边相切时,如下图,
∵PD=![]() ,∴PH=1,
,∴PH=1,
∴此时![]() ,
,
当⊙P继续向右运动,同时与AD,BC相切时,PH=1,所以此时![]() ,
,
∴当![]() 时,⊙P只与AD相切;
时,⊙P只与AD相切;
 ,
,
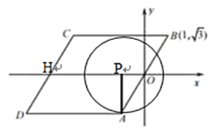
(3)当⊙P只与BC边相切时,如下图,
⊙P与AD相切于点A时,OP=1,此时m=-1,
⊙P与AD相切于点B时,OP=1,此时m=1,
∴当![]() ,⊙P只与BC边相切时;
,⊙P只与BC边相切时;
 ,
,
(4)当⊙P只与BC边相切时,如下图,
由题意可得OP=2,
∴此时![]() .
.
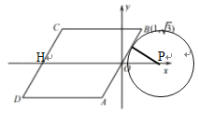
综上所述,点P的横坐标m 的取值范围![]() 或
或![]() 或
或![]() 或
或![]() .
.


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:初中数学 来源: 题型:
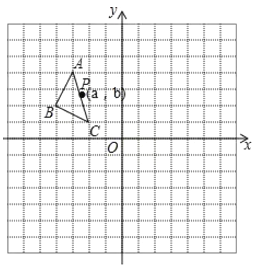
【题目】如图所示,方格纸中的每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上.
(1)将△ABC向下平移5个单位再向右平移1个单位后得到对应的△A1B1C1,画出△A1B1C1;
(2)画出△A1B1C1关于y轴对称的△A2B2C2;
(3)P(a,b)是△ABC的边AC上一点,请直接写出经过两次变换后在△A2B2C2中对应的点P2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c的图象与x轴交于A(﹣4,0)和点B两点,与y轴交于点C,抛物线的对称轴是x=﹣1与x轴交于点D.
(1)求拋物线的函数表达式;
(2)若点P(m,n)为抛物线上一点,且﹣4<m<﹣1,过点P作PE∥x轴,交抛物线的对称轴x=﹣1于点E,作PF⊥x轴于点F,得到矩形PEDF,求矩形PEDF周长的最大值;
(3)点Q为抛物线对称轴x=﹣1上一点,是否存在点Q,使以点Q,B,C为顶点的三角形是直角三角形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《函数的图象与性质》拓展学习展示:
(问题)如图1,在平面直角坐标系中,抛物线G1:![]() 与x轴相交于A(-1,0),B(3,0)两点,与y轴交于点C,则a= ,b= .
与x轴相交于A(-1,0),B(3,0)两点,与y轴交于点C,则a= ,b= .
(操作)将图1中抛物线G1沿BC方向平移BC长度的距离得到抛物线G2,G2在y轴左侧的部分与G1在y轴右侧的部分组成的新图象记为G,如图②.请直接写出图象G对应的函数解析式.
(探究)在图2中,过点C作直线l平行于x轴,与图象G交于D,E两点.求图象G在直线l上方的部分对应的函数y随x的增大而增大时x的取值范围.
(应用)P是抛物线G2对称轴上一个动点,当△PDE是直角三角形时,直接写出P点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,AB=AC,AD是BC边上的中线,点E是AD上一点,过点B作BF∥EC,交AD的延长线于点F,连接BE,CF.
(1)求证:△BDF≌△CDE;
(2)当ED与BC满足什么数量关系时,四边形BECF是正方形?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
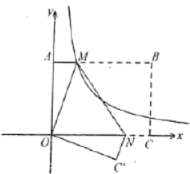
【题目】如图,在平面直角坐标系中,![]() 、
、![]() 分别为
分别为![]() 轴、
轴、![]() 轴正半轴上的点,以
轴正半轴上的点,以![]() 、
、![]() 为边,在一象限内作矩形
为边,在一象限内作矩形![]() ,且
,且![]() .将矩形
.将矩形![]() 翻折,使点
翻折,使点![]() 与原点重合,折痕为
与原点重合,折痕为![]() ,点
,点![]() 的对应点
的对应点![]() 落在第四象限,过
落在第四象限,过![]() 点的反比例函数
点的反比例函数![]()
![]() ,其图象恰好过
,其图象恰好过![]() 的中点,则点的
的中点,则点的![]() 坐标为________.
坐标为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着智能手机的普及率越来越高以及移动支付的快捷高效性,中国移动支付在世界处于领先水平.为了解人们平时最喜欢用哪种移动支付方式,因此在某步行街对行人进行随机抽样调查,以下是根据调查结果分别整理的不完整的统计表和统计图.
移动支付方式 | 支付宝 | 微信 | 其他 |
人数/人 |
| 200 | 75 |
请你根据上述统计表和统计图提供的信息.完成下列问题:
(1)在此次调查中,使用支付宝支付的人数;
(2)求表示微信支付的扇形所对的圆心角度数;
(3)某天该步行街人流量为10万人,其中30%的人购物并选择移动支付,请你依据此次调查获得的信息估计一下当天使用微信支付的人数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设![]() 都是实数,且
都是实数,且![]() .我们规定:满足不等式
.我们规定:满足不等式![]() 的实数
的实数![]() 的所有值的全体叫做闭区间、表示为
的所有值的全体叫做闭区间、表示为![]() .对于一个函数,如果它的自变量
.对于一个函数,如果它的自变量![]() 与函数值
与函数值![]() 满足:当
满足:当![]() 时,有
时,有![]() ,我们就称此函数是闭区间
,我们就称此函数是闭区间![]() 上的“闭函数”.
上的“闭函数”.
(1)反比例函数![]() 是闭区间
是闭区间![]() 上的“闭函数”吗?请判断并说明理由;
上的“闭函数”吗?请判断并说明理由;
(2)若一次函数![]() 是闭区间
是闭区间![]() 上的“闭函数”,求此一次函数的解析式;
上的“闭函数”,求此一次函数的解析式;
(3)若实数![]() 满足
满足![]() .且
.且![]() ,当二次函数
,当二次函数![]() 是闭区间
是闭区间![]() 上的“闭函数”时,求
上的“闭函数”时,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com