
【题目】如图,点E,F分别是等边△ABC中AC,AB边上的中点,以AE为边向外作等边△ADE. 
(1)求证:四边形AFED是菱形;
(2)连接DC,若BC=10,求四边形ABCD的面积.
【答案】
(1)证明:∵△ABC、△ADE是等边三角形,
∴AF=EF=AE=DE=AD,∠ACB=∠DAE=60°,
∴四边形AFED是菱形
(2)解:作AM⊥BC于M,如图所示:
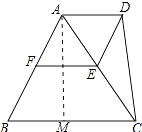
∵△ABC是等边三角形,
∴AC=BC=10,∠B=60°,
∴AM=ABsin60°=10× ![]() =5
=5 ![]() ,
,
∵E是AC的中点,
∴AE=AD= ![]() AC=5,
AC=5,
∵∠ACB=∠DAE=60°,
∴AD∥BC,
∴四边形ABCD是梯形,
∴四边形ABCD的面积= ![]() (AD+BC)×AM=
(AD+BC)×AM= ![]() (5+10)×5
(5+10)×5 ![]() =
= ![]() .
.
【解析】(1)由等边三角形的性质得出AF=EF=AE=DE=AD,由四边相等的四边形是菱形,即可得出结论;(2)作AM⊥BC于M,由等边三角形的性质和三角函数求出AM,在求出AD的长,证出四边形ABCD是梯形,由梯形的面积公式即可得出结果.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:初中数学 来源: 题型:
【题目】如图,AD、BC是⊙O的两条互相垂直的直径,点P从点O出发,沿O→C→D→O的路线匀速运动.设∠APB=y(单位:度),那么y与点P运动的时间x(单位:秒)的关系图是( )
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明有一个呈等腰直角三角形的积木盒,现在积木盒中只剩下如图1所示的九个空格,图2是可供选择的A,B,C,D四块积木. 
(1)小明选择把积木A和B放入图3,要求积木A和B的九个小圆恰好能分别与图3中的九个小圆重合,请在图3中画出他放入方式的示意图(温馨提醒:积木A和B的连接小圆的小线段还是要画上哦!);
(2)现从A、B、C、D四块积木中任选两块,请用列表法或画树状图法求恰好能全部不重叠放入的概率
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】写出下列命题的已知、求证,并完成证明过程.
命题:如果一个三角形的两条边相等,那么两条边所对的角也相等(简称:“等边对等角”.)
(1)已知: .
求证: .
(2)证明:“等边对等角”
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知⊙O的半径为5,且点O在直线l上,小明用一个三角板学具(∠ABC=90°,AB=BC=8)做数学实验:
(1)如图①,若A、B两点在⊙O上滑动,直线BC分别与⊙O,L相交于点D,E.
①求BD的长;②当OE=6时,求BE的长;
(2)如图②,当点B在直线l上,点A在⊙O上,BC与⊙O相切于点P时,则切线长PB= 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=x2+bx+c的图象与x轴交于A,B两点,与y轴交于点P,顶点为C(1,﹣2).
(1)求此函数的关系式;
(2)作点C关于x轴的对称点D,顺次连接A,C,B,D.若在抛物线上存在点E,使直线PE将四边形ACBD分成面积相等的两个四边形,求点E的坐标;
(3)在(2)的条件下,抛物线上是否存在一点F,使得△PEF是以P为直角顶点的直角三角形?若存在,求出点F的坐标及△PEF的面积;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,DE⊥BC,垂足为点E,连接AC交DE于点F,点G为AF的中点,∠ACD=2∠ACB.若DG=3,EC=1,则DE的长为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com