
| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y | … | 0 | 4 | 6 | 6 | 4 | … |
分析 根据表中数据和抛物线的对称性:可知当x=0时,y=6,当x=1时,y=6,可得对称轴为x=$\frac{0+1}{2}$=$\frac{1}{2}$;(-2,0)与(3,0)对称,即抛物线与x轴的交点为(-2,0)和(3,0);抛物线的开口向下,求得函数y=-(x-$\frac{1}{2}$)2+$\frac{25}{4}$的最大值为6.125;在对称轴左侧,y随x增大而增大.
解答 解:∵当x=0时,y=6,当x=1时,y=6,
∴对称轴为x=$\frac{0+1}{2}$=$\frac{1}{2}$;
∴(-2,0)与(3,0)对称,
∴抛物线与x轴的一个交点为(3,0),
设抛物线解析式为y=a(x-$\frac{1}{2}$)2+k,代入(-2,0),0,6)求得函数y=-(x-$\frac{1}{2}$)2+$\frac{25}{4}$,
∵抛物线的开口向下,
∴函数的最大值为6.125;在对称轴左侧,y随x增大而增大;
正确的是①②③④.
故答案为:①②③④.
点评 本题考查了抛物线y=ax2+bx+c的性质:抛物线是轴对称图形,它与x轴的两个交点是对称点,对称轴与抛物线的交点为抛物线的顶点;a<0时,函数有最大值,在对称轴左侧,y随x增大而增大.


科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
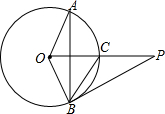 如图,已知P是⊙O外一点,PO交圆O于点C,OC=CP=2,弦AB⊥OC,∠AOB=120°,连接PB.
如图,已知P是⊙O外一点,PO交圆O于点C,OC=CP=2,弦AB⊥OC,∠AOB=120°,连接PB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com