
【题目】如图,已知一条直线过点![]() ,且与抛物线
,且与抛物线![]() 交于
交于![]() 两点,其中点
两点,其中点![]() 的横坐标是
的横坐标是![]() .
.
⑴求这条直线的函数关系式及点![]() 的坐标 ;
的坐标 ;
⑵在![]() 轴上是否存在点
轴上是否存在点![]() ,使得△
,使得△![]() 是直角三角形?若存在,求出点
是直角三角形?若存在,求出点![]() 的坐标,若不存在,请说明理由;
的坐标,若不存在,请说明理由;
⑶过线段![]() 上一点
上一点![]() ,作
,作![]() ∥
∥![]() 轴,交抛物线于点
轴,交抛物线于点![]() ,点
,点![]() 在第一象限;点
在第一象限;点![]() ,当点
,当点![]() 的横坐标为何值时,
的横坐标为何值时, ![]() 的长度最大?最大值是多少?
的长度最大?最大值是多少?

【答案】(1)点![]() 的坐标为
的坐标为![]() ;(2)
;(2)![]() ;(3)当
;(3)当![]() 的横坐标为6时,
的横坐标为6时, ![]() 的长度最大值为18.
的长度最大值为18.
【解析】⑴关键是求直线的解析式,由于直线上有一点为![]() ,所以再找一个点即可求出直线的解析式;
,所以再找一个点即可求出直线的解析式; ![]() 的横坐标是
的横坐标是![]() 代入抛物线的解析式即可求出它的纵坐标,利用待定系数法可求直线的函数关系式;由于点
代入抛物线的解析式即可求出它的纵坐标,利用待定系数法可求直线的函数关系式;由于点![]() 是两个函数图象的交点,所以把两个函数联立起来,利用方程思想可以解决问题.
是两个函数图象的交点,所以把两个函数联立起来,利用方程思想可以解决问题.
⑵先假设存在,在假设存在的情况下还要分类讨论,因为没有指明直角顶点,所以要分成三种情况来讨论,利用勾股定理建立方程可以解决问题.
⑶利用![]() 的横坐标分别表示出线段
的横坐标分别表示出线段![]() 的长度,再利用
的长度,再利用![]() 建立函数关系,再根据函数关系来求最值.
建立函数关系,再根据函数关系来求最值.
解:⑴∵直线与抛物线交点![]() 的横坐标是
的横坐标是![]() ,
,
∴![]() ,
,
∴点![]() 的坐标是
的坐标是![]()
设此直线的解析式为![]() ,
,
将![]() 代入得
代入得![]() ,
,
解得: 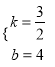 ,
,
∴此直线的解析式为![]() .
.
∵直线和抛物线交于![]() 两点,
两点,
∴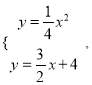
解得: ![]() 或
或![]()
∴点![]() 的坐标为
的坐标为![]() .
.
⑵.如备用图,点![]() 在
在![]() 轴上,连接
轴上,连接![]() .
.
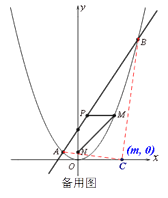
∵![]() 的坐标是
的坐标是![]() ,点
,点![]() 的坐标为
的坐标为![]() ,
,
∴![]() ,
,
若设存在的点![]() 的坐标为
的坐标为![]() ,则:
,则:
![]() ,
,
![]() ,
,
①.当![]() 时,
时, ![]() ,即
,即![]() ,
,
解得: ![]() .
.
②.当![]() 时,
时, ![]() ,即
,即![]()
解得: ![]() 或
或![]() .
.
③.当![]() 时,
时, ![]() ,即
,即![]()
解得: ![]() .
.
∴求出点![]() 的坐标为
的坐标为![]() .
.
⑶.设点![]() ,设
,设![]() 与
与![]() 轴的交点为
轴的交点为![]() ;
;
在![]() △
△![]() 中,由勾股定理的:
中,由勾股定理的: 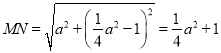 ,
,
又∵点![]() 与点
与点![]() 的纵坐标相同,∴
的纵坐标相同,∴![]() ,
,
∴![]() ,即点
,即点![]() 的横坐标为
的横坐标为![]() ,
,
∴![]() ,
,
∴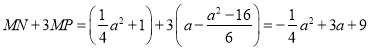 ,
,
∴当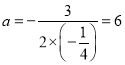 时,又∵
时,又∵![]() ,取值最大值取到18.
,取值最大值取到18.
∴当![]() 的横坐标为6时,
的横坐标为6时, ![]() 的长度最大值为18.
的长度最大值为18.


科目:初中数学 来源: 题型:
【题目】如图,矩形纸片ABCD中,已知AD =8,折叠纸片使AB边与对角线AC
重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为( )

A. 3 B. 4
C. 5 D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】快递公司准备购买机器人来代替人工分拣已知购买- 台甲型机器人比购买-台乙型机器人多![]() 万元;购买
万元;购买![]() 台甲型机器人和
台甲型机器人和![]() 台乙型机器人共需
台乙型机器人共需![]() 万元.
万元.
(1)求甲、乙两种型号的机器人每台的价格各是多少万元;
(2)已知甲型、乙型机器人每台每小时分拣快递分别是![]() 件、
件、![]() 件,该公司计划最多用
件,该公司计划最多用![]() 万元购买
万元购买![]() 台这两种型号的机器人.该公司该如何购买,才能使得每小时的分拣量最大?
台这两种型号的机器人.该公司该如何购买,才能使得每小时的分拣量最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,AO⊥BC,垂足为点O,⊙O与AC相切于点D,BE⊥AB交AC的延长线于点E,与⊙O相交于G、F两点.
(1)求证:AB与⊙O相切;
(2)若等边三角形ABC的边长是8,求线段BF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用“”规定一种新运算:对于任意有理数a和b,规定ab=ab2+2ab+a.如:13=1×32+2×1×3+1=16
(1)求2(-1)的值;
(2)若(a+1)3=32,求a的值;
(3)若m=2x,n=(![]() x)3(其中x为有理数),试比较m、n的大小.
x)3(其中x为有理数),试比较m、n的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某次考试中,某班级的数学成绩统计图如图.下列说法错误的是( )

A. 得分在70~80分之间的人数最多 B. 该班的总人数为40
C. 得分在90~100分之间的人数最少 D. 及格(≥60分)人数是26
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数填在相应的大括号内:
﹣5,|-![]() |,﹣12,0,﹣3.14,+1.99,﹣(﹣6),
|,﹣12,0,﹣3.14,+1.99,﹣(﹣6),![]()
(1)正数集合:{ …}
(2)负数集合:{ …}
(3)整数集合:{ …}
(4)分数集合:{ …}.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 的图象与
的图象与![]() 轴有两个公共点.
轴有两个公共点.
(1)求![]() 的取值范围,写出当
的取值范围,写出当![]() 取其范围内最大整数时抛物线的解析式;
取其范围内最大整数时抛物线的解析式;
(2)将(1)中所求得的抛物线记为![]() ,
,
①求![]() 的顶点
的顶点![]() 的坐标;
的坐标;
②若当![]() 时,
时, ![]() 的取值范围是
的取值范围是![]() ,求
,求![]() 的值;
的值;
(3)将![]() 平移得到抛物线
平移得到抛物线![]() ,使
,使![]() 的顶点
的顶点![]() 落在以原点为圆心半径为
落在以原点为圆心半径为![]() 的圆上,求点
的圆上,求点![]() 与
与![]() 两点间的距离最大时
两点间的距离最大时![]() 的解析式,怎样平移
的解析式,怎样平移![]() 可以得到所求抛物线?
可以得到所求抛物线?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com