
 2015年5月中旬,中国和俄罗斯海军在地中海海域举行了代号为“海上联合-2015(1)”的联合军事演习,这是中国第一次地中海举行军事演习,也是这个海军距本土最远的一次军演,某天,“临沂舰”、“潍坊舰”两舰同时从A、B两个港口出发,均沿直线匀速驶向演习目标地海岛C,两舰艇都到达C岛后演习第一阶段结束,已知B刚位于A港、C岛之间,且A、B、C在一条直线上,如图所示,l临、l潍分别表示“临沂舰”、“潍坊舰”离B港的距离行驶时间x(h)变化的图象.
2015年5月中旬,中国和俄罗斯海军在地中海海域举行了代号为“海上联合-2015(1)”的联合军事演习,这是中国第一次地中海举行军事演习,也是这个海军距本土最远的一次军演,某天,“临沂舰”、“潍坊舰”两舰同时从A、B两个港口出发,均沿直线匀速驶向演习目标地海岛C,两舰艇都到达C岛后演习第一阶段结束,已知B刚位于A港、C岛之间,且A、B、C在一条直线上,如图所示,l临、l潍分别表示“临沂舰”、“潍坊舰”离B港的距离行驶时间x(h)变化的图象.分析 (1)从图象可以看出A港与C岛之间的距离为A、B间的距离+B、C间的距离就可以求出结论;
(2)根据A、B之间的距离和行驶时间可以求出其速度,就可以求出从B到C的时间,从而求出a,根据图象求出l临、l潍的解析式,然后由其解析式构成方程组求出其解就可以得出“临沂舰”、“潍坊舰”的航速即相遇时行驶的时间;
(2)分两种情况列出方程求出其解就可以得出答案.
解答 解:(1)由图象,得
A港与C岛之间的距离为:200km;
故答案为:200km;
(2)“临沂舰”的航速:40÷0.5=80(km/h),
“潍坊舰”的航速:160÷2$\frac{2}{3}$=60(km/h),
a=0.5+160÷80=2.5,
设l潍的解析式为y2=k2x,l临的解析式为y1=k1x+b1,由图象得,
160=3$\frac{2}{3}$k2,$\left\{\begin{array}{l}{0=0.5{k}_{1}+{b}_{1}}\\{160=2.5{k}_{1}+{b}_{1}}\end{array}\right.$,
解得:k2=60,$\left\{\begin{array}{l}{{k}_{1}=80}\\{{b}_{1}=-40}\end{array}\right.$,
∴y2=60x,y1=80x-40,
当y1=y2时,
60x=80x-40,
x=2,
∴相遇时行驶的时间为2h;
(3)当y2-y1=2时,则60x-(80x-40)=2,
解得x=$\frac{19}{10}$,
当y1-y2=2时,则(80x-40)-60x=2,
解得x=$\frac{21}{10}$
∴处于最佳通讯距离时的x的取值范围为$\frac{19}{10}$≤x≤$\frac{21}{10}$.
点评 本题考查了一次函数的应用,待定系数法求函数的解析式以及函数的解析式与一元一次方程的运用,在解答时求出函数的解析式是关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
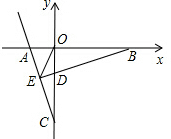 在平面直角坐标系中,已知点A(a,0),C(0,b),且a、b满足(a+1)2+$\sqrt{b+3}$=0.
在平面直角坐标系中,已知点A(a,0),C(0,b),且a、b满足(a+1)2+$\sqrt{b+3}$=0.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{6}$ | B. | 3$\sqrt{5}$ | C. | $\sqrt{3}$ | D. | $\sqrt{8}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com