
分析 (1)根据同底数幂的乘法进行计算即可解答本题;
(2)根据幂的乘方和同底数幂的乘法可以解答本题;
(3)根据同底数幂的乘法进行计算即可解答本题;
(4)根据积的乘方和同底数幂的乘法进行计算即可解答本题;
(5)根据积的乘方和同底数幂的乘法进行计算即可解答本题;
(6)根据积的乘方和同底数幂的乘法进行计算即可解答本题;
(7)根据同底数幂的乘法进行计算即可解答本题;
(8)根据提公因式法和完全平方公式可以解答本题.
解答 解:(1)2x•$\frac{2}{7}$xy=$\frac{4}{7}$x2y;
(2)(-2a)•(-$\frac{5}{2}$ab)2
=(-2a)($\frac{25}{4}$a2b2)
=-$\frac{25}{2}$a3b2;
(3)3a2•(-7ab)=-21a3b;
(4)(-3xy)3•($\frac{1}{27}$xz)
=(-27x3y3)($\frac{1}{27}$xz)
=-x4y3z;
(5)(-xy)2•(2xz)2
=x2y2•(4x2z2)
=4x4y2z2;
(6)(-2ab)•5ab3•(-$\frac{3}{5}$a2b2)
=(2×5×$\frac{3}{5}$)(a•a•a2)(b•b3•b2)
=6a4b6;
(7)(-a-b)5(a+b)3
=-(a+b)5(a+b)3
=-(a+b)8;
(8)[(a+b)2•(a-b)3]-(b-a)5
=(a+b)2•(a-b)3+(a-b)5
=(a-b)3[(a+b)2+(a-b)2]
=2(a-b)3(a2+b2);
故答案为:(1)$\frac{4}{7}$x2y;(2)-$\frac{25}{2}$a3b2;(3)-21a3b;(4)-x4y3z;(5)4x4y2z2;(6)6a4b6;(7)-(a+b)8;(8)2(a-b)3(a2+b2).
点评 本题考查整式的混合运算,解题的关键是明确整式的混合运算的计算方法.


 阶梯计算系列答案
阶梯计算系列答案科目:初中数学 来源: 题型:解答题
 某中学八(1)班共50名同学开展了“我为灾区献爱心”捐款活动.小明将捐款情况进行了统计,并绘制成如图的条形统计图.
某中学八(1)班共50名同学开展了“我为灾区献爱心”捐款活动.小明将捐款情况进行了统计,并绘制成如图的条形统计图.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
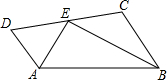 已知,如图,AD∥BC,AE平分∠BAD,BE平分∠ABC,求证:AD+BC=AB.
已知,如图,AD∥BC,AE平分∠BAD,BE平分∠ABC,求证:AD+BC=AB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com