
| A�� | 6 | B�� | 24 | C�� | 30 | D�� | 120 |
���� ����ʽ����κ�����ȷ����a�ķ�Χ���ٱ�ʾ����ʽ���̵Ľ⣬�ɷ�ʽ�����������⣬ȷ��������������������a��ֵ��������������
��� �⣺����ʽ�������ã�$\left\{\begin{array}{l}{x��a-1}\\{x��4}\end{array}\right.$��
�ɲ���ʽ���⣬�õ�a-1��4����a��5��
a��ֵΪ1��2��3��4��5��
��ʽ����ȥ��ĸ�ã�4x-2a=x-2��
��ã�x=$\frac{2a-2}{3}$����$\frac{2a-2}{3}$��2��
��x=$\frac{2a-2}{3}$��0��
��2a-2��0��
��ã�a��1��
��a=1��2��3��5��
����������������a��ֵ֮����30��
��ѡC��
���� ���⿼���˷�ʽ���̵Ľ⣬�Լ���һԪһ�β���ʽ���飩�������������㷨���ǽⱾ��Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-1��3�� | B�� | ��1��3�� | C�� | ��-3��3�� | D�� | ��-1��5�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
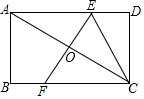 ��ͼ���ھ���ABCD�У�AB=3����BCA=30�㣬�Խ���AC�Ĵ�ֱƽ���߷ֱ�AD��BC�ڵ�E��F������CE����CE�ij�Ϊ2$\sqrt{3}$��
��ͼ���ھ���ABCD�У�AB=3����BCA=30�㣬�Խ���AC�Ĵ�ֱƽ���߷ֱ�AD��BC�ڵ�E��F������CE����CE�ij�Ϊ2$\sqrt{3}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 Ϊ�˷ḻ�����ͯ��ҵ�����ij����Ҫ������ͼ��AB�Ͻ�һ��ͼ����P��������������ѧУ�����ڵ�λ��Ϊ��C�͵�D����CA��AB�ڵ�A��DB��AB�ڵ�B����֪AB=25km��DB=10km��CA=15km��Ҫ��ͼ����P������ѧУ�ľ�����ȣ�
Ϊ�˷ḻ�����ͯ��ҵ�����ij����Ҫ������ͼ��AB�Ͻ�һ��ͼ����P��������������ѧУ�����ڵ�λ��Ϊ��C�͵�D����CA��AB�ڵ�A��DB��AB�ڵ�B����֪AB=25km��DB=10km��CA=15km��Ҫ��ͼ����P������ѧУ�ľ�����ȣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
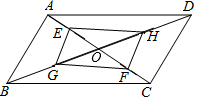 ��ͼ��ƽ���ı���ABCD�ĶԽ���AC��BD���ڵ�O��E��F��AC�ϣ�G��H��BD�ϣ���AE=CF��BG=DH����֤��GF=HE��
��ͼ��ƽ���ı���ABCD�ĶԽ���AC��BD���ڵ�O��E��F��AC�ϣ�G��H��BD�ϣ���AE=CF��BG=DH����֤��GF=HE���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
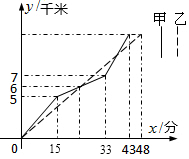 ��ͼ��ʾ�ס�������ͬѧ�ڡ��壮һ���Ű������г����С�������·��y��ǧ�ף���ʱ��x���֣��仯��ͼ��ȫ�̣�������ͼ��ش��������⣮
��ͼ��ʾ�ס�������ͬѧ�ڡ��壮һ���Ű������г����С�������·��y��ǧ�ף���ʱ��x���֣��仯��ͼ��ȫ�̣�������ͼ��ش��������⣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com