
(本题满分18分)已知二次函数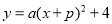 的图象是由函数
的图象是由函数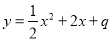 的图象向左平移一个单位得到.反比例函数
的图象向左平移一个单位得到.反比例函数 与二次函数
与二次函数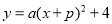 的图象交于点A(1,n).
的图象交于点A(1,n).
(1)求a,p,q,m,n的值;
(2)要使反比例函数和二次函数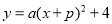 在直线
在直线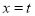 的一侧都是y随着x的增大而减小,求t的最大值;
的一侧都是y随着x的增大而减小,求t的最大值;
(3)记二次函数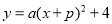 图象的顶点为B,以AB为边构造矩形ABCD,边CD与函数
图象的顶点为B,以AB为边构造矩形ABCD,边CD与函数 相交,且直线AB与CD的距离为
相交,且直线AB与CD的距离为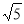 ,求出点D,C的坐标.
,求出点D,C的坐标.
【解析】
(1)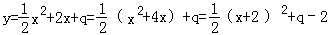 ,顶点坐标(﹣2,q﹣2)
,顶点坐标(﹣2,q﹣2)
(或用顶点坐标公式)
∴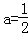 ,p=3,q=6,
,p=3,q=6,
把x=1,y=n代入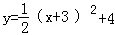 得n=12;
得n=12;
把x=1,y=12代入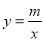 得m=12;
得m=12;
(2)∵反比例函数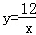 在图象所在的每一象限内,y随着x的增大而减小
在图象所在的每一象限内,y随着x的增大而减小
而二次函数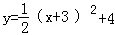 的对称轴为:直线x=﹣3
的对称轴为:直线x=﹣3
要使二次函数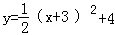 满足上述条件,x≤﹣3
满足上述条件,x≤﹣3
∴t的最大值为﹣3;
(3)如图,过点A作直线l∥x轴,作DF⊥l于F,BE⊥l于E.
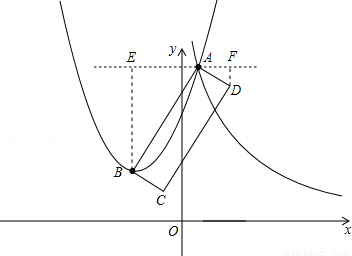
∵点B的坐标为(﹣3,4),A(1,12)
∴AE=4,BE=8
∵BE⊥l,
∴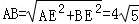 ;
;
∵四边形ABCD是矩形,
∴∠BAD=90°,
∴∠EAB+∠FAD=90°
∵BE⊥l于E,
∴∠EAB+∠EBA=90°
∴∠FAD=∠EBA
∴Rt△EBA∽Rt△FAD
∴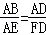
又∵AD=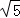 ,
,
∴FD=1
同理:AF=2
【解析】
试题分析:(1)先将函数y= x2+2x+q配方,即可得到顶点坐标(-2,q-2),根据平移的性质可得a=
x2+2x+q配方,即可得到顶点坐标(-2,q-2),根据平移的性质可得a= ,p=3,q=6,再把x=1,y=n代入y=
,p=3,q=6,再把x=1,y=n代入y= (x+3)2+4,把x=1,y=12代入
(x+3)2+4,把x=1,y=12代入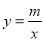 可求m,n的值;(2)根据反比例函数的增减性,二次函数y=
可求m,n的值;(2)根据反比例函数的增减性,二次函数y= (x+3)2+4的对称轴和增减性,即可求得t的最大值;(3)过点A作直线l∥x轴,作DF⊥l于F,BE⊥l于E.,根据勾股定理,矩形的性质,相似三角形的判定和性质,即可求得点D,C的坐标.
(x+3)2+4的对称轴和增减性,即可求得t的最大值;(3)过点A作直线l∥x轴,作DF⊥l于F,BE⊥l于E.,根据勾股定理,矩形的性质,相似三角形的判定和性质,即可求得点D,C的坐标.
考点:二次函数综合题.


科目:初中数学 来源:2014-2015学年河北省深州市九年级上学期第三次月考数学试卷(解析版) 题型:填空题
小明在学习“锐角三角函数”中发现,将如图的矩形纸片ABCD沿过点B的直线折叠,使点A落在BC上的点E处,还原后,再沿过点E的直线折叠,使点A落在BC上的点F处,这样就可以求出67.5°角的正切值为 .
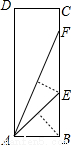
查看答案和解析>>
科目:初中数学 来源:2014-2015学年河北省定州市九年级上学期期中考试数学试卷(解析版) 题型:选择题
已知点(1,2)在抛物线y=ax2+1上,则下列各点也在此抛物线上的是( )
A.(2,1) B.(﹣2,1) C.(1,﹣2) D.(﹣1,2)
查看答案和解析>>
科目:初中数学 来源:2014-2015学年福建省九年级上学期期中考试数学试卷(解析版) 题型:填空题
已知Rt△ABC中,∠C=900,AC=4,BC=7, 则∠B ≈ 。 (精确到1’)
查看答案和解析>>
科目:初中数学 来源:2014-2015学年福建省九年级上学期期中考试数学试卷(解析版) 题型:选择题
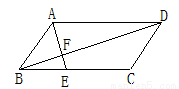
如图,F是平行四边形ABCD对角线BD上的点,BF∶FD=1∶3,则BE∶EC=( )
A.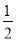 B.
B.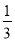 C.
C.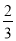 D.
D.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年福建省龙岩市分校九年级上学期第三次阶段考试数学试卷(解析版) 题型:解答题
已知点P(1,-2a)在二次函数y=ax2+6的图象上,并且点P关于x轴的对称点在反比例函数 的图象上。
的图象上。
(1)求此二次函数和反比例函数的解析式;
(2)点(-1,4)是否同时在(1)中的两个函数图象上?
查看答案和解析>>
科目:初中数学 来源:2014-2015学年福建省福安市小片区九年级上学期半期考试数学试卷(解析版) 题型:解答题
(本题每小题8分,共16分)
(1)(x+1)2=2
(2)x2-2x-3=0 (用适当的方法)
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市平谷区九年级上学期期末考试数学试卷(解析版) 题型:选择题
在Rt△ABC中,∠C=90°,AC=4,BC=3,则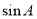 是
是
A. B.
B.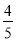 C.
C.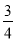 D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com