
【题目】如图,一次函数y1=x+4的图象与反比例函数y2=![]() 的图象交于A(﹣1,a),B两点,与x轴交于点C.
的图象交于A(﹣1,a),B两点,与x轴交于点C.
(1)求k.
(2)根据图象直接写出y1>y2时,x的取值范围.
(3)若反比例函数y2=![]() 与一次函数y1=x+4的图象总有交点,求k的取值.
与一次函数y1=x+4的图象总有交点,求k的取值.

【答案】(1)-3;(2)﹣3<x<﹣1;(3)k≥﹣4且k≠0.
【解析】
(1)把点A坐标代入一次函数关系式可求出a的值,确定点A的坐标,再代入反比例函数关系式可求出k的值,
(2)一次函数与反比例函数联立,可求出交点B的坐标,再根据图象可得出当y1>y2时,x的取值范围.
(3)若反比例函数y2=![]() 与一次函数y1=x+4的图象总有交点,就是x2+4x﹣k=0有实数根,根据根的判别式求出k的取值范围.
与一次函数y1=x+4的图象总有交点,就是x2+4x﹣k=0有实数根,根据根的判别式求出k的取值范围.
(1)一次函数y1=x+4的图象过A(﹣1,a),
∴a=﹣1+4=3,
∴A(﹣1,3)代入反比例函数y2=![]() 得,
得,
k=﹣3;
(2)由(1)得反比例函数![]() ,由题意得,
,由题意得,
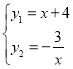 ,解得,
,解得,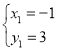 ,
,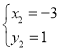 ,
,
∴点B(﹣3,1)
当y1>y2,即一次函数的图象位于反比例函数图象上方时,
自变量的取值范围为:﹣3<x<﹣1;
(3)若反比例函数y2=![]() 与一次函数y1=x+4的图象总有交点,
与一次函数y1=x+4的图象总有交点,
即,方程![]() =x+4有实数根,也就是x2+4x﹣k=0有实数根,
=x+4有实数根,也就是x2+4x﹣k=0有实数根,
∴16+4k≥0,
解得,k≥﹣4,
∵k≠0,
∴k的取值范围为:k≥﹣4且k≠0.


科目:初中数学 来源: 题型:
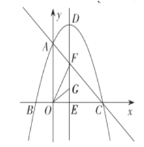
【题目】如图,矩形AOBC放置在平面直角坐标系xOy中,边OA在y轴的正半轴上,边OB在x轴的正半轴上,抛物线的顶点为F,对称轴交AC于点E,且抛物线经过点A(0,2),点C,点D(3,0).∠AOB的平分线是OE,交抛物线对称轴左侧于点H,连接HF.
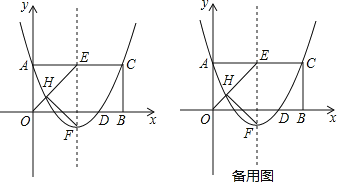
(1)求该抛物线的解析式;
(2)在x轴上有动点M,线段BC上有动点N,求四边形EAMN的周长的最小值;
(3)该抛物线上是否存在点P,使得四边形EHFP为平行四边形?如果存在,求出点P的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“用频率估计概率”的实验中,统计了某种结果出现的频率,绘制了下面的折线图,那么符合这一结果的实验最有可能的是( )
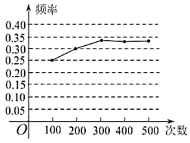
A.洗匀后的1张红桃,2张黑桃牌,从中随机抽取一张牌是黑桃
B.“石头、剪刀、布”的游戏,小王随机出的是“剪刀”
C.掷一枚质地均匀的硬币,落地时结果是“正面向上”
D.掷一个质地均匀的正六面体骰子,落地时朝上面的点数是6
查看答案和解析>>
科目:初中数学 来源: 题型:
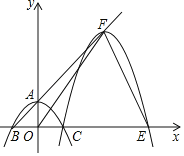
【题目】如图,抛物线y=ax2+c(a≠0)与y轴交于点A,与x轴交于B,C两点(点C在x轴正半轴上),△ABC为等腰直角三角形,且面积为4,现将抛物线沿BA方向平移,平移后的抛物线过点C时,与x轴的另一交点为E,其顶点为F.
(1)求a、c的值;
(2)连接OF,试判断△OEF是否为等腰三角形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
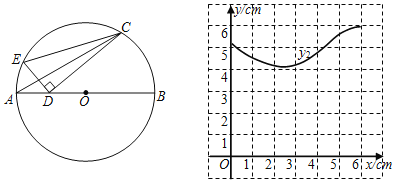
【题目】如图,AB是圆O的直径,点C是圆O上一点,∠CAB=30°,D是直径AB上一动点,连接CD并过点D作CD的垂线,与圆O的其中一个交点记为点E(点E位于直线CD上方或左侧),连接EC.已知AB=6cm,设A、D两点间的距离为xcm,C、D两点间的距离为y1cm,E、C两点间的距离为y2cm,小雪根据学习函数的经验,分别对函数y1,y2随自变量x的变化而变化的规律进行了探究.下面是小雪的探究过程:
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y1/cm | 5.2 | 4.4 | 3.6 | 3.0 | 2.7 | 2.7 |
|
y2/cm | 5.2 | 4.6 | 4.2 |
| 4.8 | 5.6 | 6.0 |
(1)按照下表中自变量x的值进行取点、面图、测量,分别得到了y1,y2与x的几组对应值,请将表格补充完整:(保留一位小数)
(2)在同一平面直角坐标系xOy中,y2的图象如图所示,描出补全后的表中各组数值所对应的点(x,y1),(x,y2),并画出函数y1的图象;
(3)结合函数图象,解决问题:当∠ECD=60°时,AD的长度约为 cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上,
上,![]() ,连接
,连接![]() ,
,![]() .动点
.动点![]() 在
在![]() 上从点
上从点![]() 向终点
向终点![]() 匀速运动,同时,动点
匀速运动,同时,动点![]() 在射线
在射线![]() .上从点
.上从点![]() 沿
沿![]() 方向匀速运动,当点
方向匀速运动,当点![]() 运动到EF的中点时,点
运动到EF的中点时,点![]() 恰好与点
恰好与点![]() 重合,点
重合,点![]() 到达终点时,
到达终点时,![]() ,
, ![]() 同时停止运动.
同时停止运动.
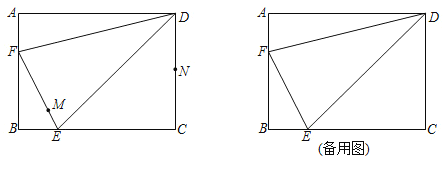
(1)求![]() 的长.
的长.
(2)设![]() ,
,![]() ,求
,求![]() 关于
关于![]() 的函数表达式,并写出自变
的函数表达式,并写出自变![]() 的取值范围.
的取值范围.
(3)连接![]() ,当
,当![]() 与
与![]() 的一边平行时,求
的一边平行时,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究
如图,在平面直角坐标系中,点![]() 为坐标原点,抛物线
为坐标原点,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,
,![]() ,抛物线的对称轴交抛物线于点
,抛物线的对称轴交抛物线于点![]() ,交
,交![]() 轴于点
轴于点![]() ,交直线
,交直线![]() 于点
于点![]() .
.
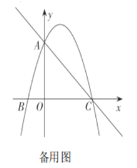
(1)求抛物线的函数表达式及其对称轴:
(2)点![]() 是线段
是线段![]() 上一点,且
上一点,且![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)若点![]() 是抛物线上任意一点,点
是抛物线上任意一点,点![]() 是直线
是直线![]() 上任意一点,点
上任意一点,点![]() 是平面上任意一点,是否存在这样的点
是平面上任意一点,是否存在这样的点![]() ,
,![]() ,
,![]() ,使得以点
,使得以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是正方形,若存在,请直接写出点
为顶点的四边形是正方形,若存在,请直接写出点![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
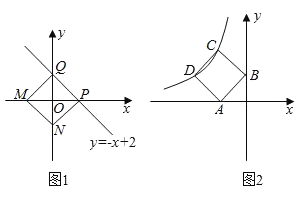
【题目】已知:点M、N分别是x轴y轴上的动点,点P、Q是某个函数图象上的点,当四边形MNPQ为正方形时,称这个正方形为此函数的“梦幻正方形”例如:如图1所示,正方形MNPQ是一次函数y=﹣x+2的其中一个“梦幻正方形”.
(1)若某函数是y=x+5,求它的图象的所有“梦幻正方形”的边长;
(2)若某函数是反比例函数y=![]() (k<0)(如图2所示),它的图象的“梦幻正方形”ABCD,D(﹣4,m)(m<4)在反比例函数图象上,求m的值及反比例函数的解析式.
(k<0)(如图2所示),它的图象的“梦幻正方形”ABCD,D(﹣4,m)(m<4)在反比例函数图象上,求m的值及反比例函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△ADE是两个不全等的等腰直角三角形,其中点B与点D是直角顶点,现固定△ABC,而将△ADE绕点A在平面内旋转.
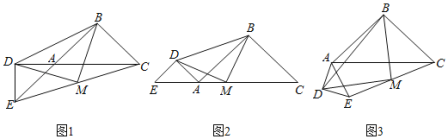
(1)如图1,当点D在CA延长线上时,点M为EC的中点,求证:△DMB是等腰三角形.
(2)如图2,当点E在CA延长线上时,M是EC上一点,若△DMB是等腰直角三角形,∠DMB为直角,求证:点M是EC的中点.
(3)如图3,当△ADE绕点A旋转任意角度时,线段EC上是否都存在点M,使△BMD为等腰直角三角形,若不存在,请举出反例;若存在,请予以证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com