
【题目】定义:点![]() 到图形
到图形![]() 上每一个点的距离的最小值称为点
上每一个点的距离的最小值称为点![]() 到图形
到图形![]() 的距离.例如,如图1,正方形
的距离.例如,如图1,正方形![]() 满足
满足![]() ,
,![]() ,
,![]() ,
,![]() ,那么点
,那么点![]() 到正方形
到正方形![]() 的距离为
的距离为![]() .
.

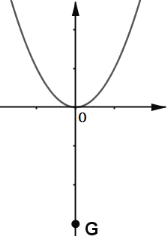
(1)如果点![]()
![]() 到抛物线
到抛物线![]() 的距离为
的距离为![]() ,请直接写出
,请直接写出![]() 的值________.
的值________.
(2)求点![]() 到直线
到直线![]() 的距离.
的距离.
(3)如果点![]() 在直线
在直线![]() 上运动,并且到直线
上运动,并且到直线![]() 的距离为
的距离为![]() ,求
,求![]() 的坐标.
的坐标.
【答案】(1)b=-3;(2)![]() 到直线
到直线![]() 的距离为
的距离为![]() ;(3)(2, 6-
;(3)(2, 6-![]() )或
)或
(2, 6+![]() )
)
【解析】
(1)作草图可知,当G在原点下方时,b=-3;
(2)过点M作直线y=x+3的垂线,与直线y=x+3相交于点H,则线段MH的长即为点M到直线y=x+3的距离.由等腰直角三角形MH=![]() ME求解即可;
ME求解即可;
(3)分N 在直线y=x+4的上方和下方求解即可.
解:(1)由图可知线段GO长即为点G到抛物线![]() 的距离,故GO=3,所以b=-3
的距离,故GO=3,所以b=-3
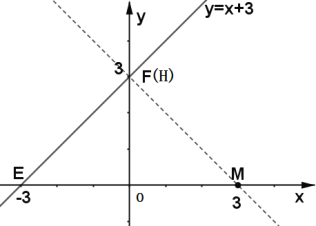
(2)如图,直线y=x+3与x,y轴分别交于点E(-3,0),F(0,3),直线y=x+3与x轴所成的角为45°,过点M作MH⊥EF,交EF与H,线段MH的长度即为点M到直线y=x+3的距离,且易知H点与F点重合.
∵![]() 为等腰直角三角形,
为等腰直角三角形,
∴EM=![]() FM ,
FM ,
又∵EF=3-(-3)=6,
∴MF=![]() EM=
EM=![]() ×6=3
×6=3![]()
∴MH=3![]()
即点![]() 到直线
到直线![]() 的距离为
的距离为![]() ;
;
(3)如图
K为直线x=2与x轴的交点,故K(2,0),F为直线x=2和直线y=x+4的交点,故F(2,6)
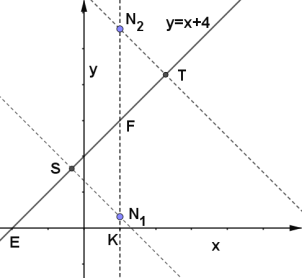
①当点N在直线y=x+4的下方N1处时,过点N1作N1S垂直直线y=x+4,
∵点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,
,
∴SN1=4,
点E是直线y=x+4与x轴的交点,
∴E(-4,0),且∠FEK=45°,
∴![]() 为等腰直角三角形
为等腰直角三角形
∴EK=FK=2-(-4)=6,
F N1=![]() N1S=
N1S=![]() ,
,
∴KN1=FK- F N1=6-![]() ,
,
∴N1(2, 6-![]() )
)
②当点N在直线y=x+4的上方N2处时,过点N2作N2T垂直直线y=x+4,
同理可得:N2T=4,N2F= ![]() N2T=
N2T=![]() ,
,
∴N2K=KF+FN2=6+![]() ,
,
∴N2(2, 6+![]() )
)
故点![]() 在直线
在直线![]() 上运动,并且到直线
上运动,并且到直线![]() 的距离为
的距离为![]() ,
,![]() 的坐标为(2, 6-
的坐标为(2, 6-![]() )或
)或
(2, 6+![]() ).
).


科目:初中数学 来源: 题型:
【题目】河南省开封市铁塔始建于公元1049年(北宋皇祐元年),是国家重点保护文物之一,在900多年中,历经了数次地震、大风、水患而巍然屹立,素有“天下第一塔”之称.如图,小明在铁塔一侧的水平面上一个台阶的底部A处测得塔顶P的仰角为45°,走到台阶顶部B处,又测得塔顶P的仰角为38.7°,已知台阶的总高度BC为3米,总长度AC为10米,试求铁塔的高度.(结果精确到1米,参考数据:sin38.7°≈0.63,cos38.7°≈0.78,tan38.7°≈0.80)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学兴趣小组同学进行测量大树CD高度的综合实践活动,如图,在点A处测得直立于地面的大树顶端C的仰角为36°,然后沿在同一剖面的斜坡AB行走13米至坡顶B处,然后再沿水平方向行走6米至大树脚底点D处,斜面AB的坡度(或坡比)i=1:2.4,求大树CD的高度?(参考数据:sin36°≈0.59,cos36°≈0.81,tan36°≈0.73)
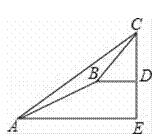
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形 ABCD 中, G 为 BC 边上一点, BE AG 于 E , DF AG 于 F ,连接 DE .
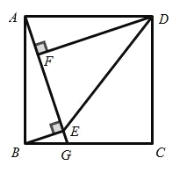
(1)求证: ABE DAF ;
(2)若 AF 1,四边形 ABED 的面积为6 ,求 EF 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了增强学生体质,决定开设以下体育课外活动项目:A:篮球 B:乒乓球C:羽毛球 D:足球,为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,请回答下列问题:


(1)这次被调查的学生共有 人;
(2)请你将条形统计图(2)补充完整;
(3)在平时的乒乓球项目训练中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学中任选两名参加乒乓球比赛,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() 与
与![]() 轴和
轴和![]() 轴分别交于点
轴分别交于点![]() 和点
和点![]() 抛物线
抛物线![]() 经过点
经过点![]() 与直线
与直线![]() 的另一个交点为
的另一个交点为![]() .
.
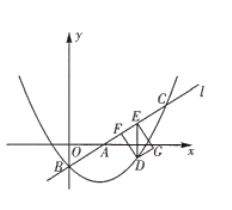
![]() 求
求![]() 的值和抛物线的解析式
的值和抛物线的解析式
![]() 点
点![]() 在抛物线上,
在抛物线上,![]() 轴交直线
轴交直线![]() 于点
于点![]() 点
点![]() 在直线
在直线![]() 上,且四边形
上,且四边形![]() 为矩形.设点
为矩形.设点![]() 的横坐标为
的横坐标为![]() 矩形
矩形![]() 的周长为
的周长为![]() 求
求![]() 与
与![]() 的函数关系式以及
的函数关系式以及![]() 的最大值
的最大值
![]() 将
将![]() 绕平面内某点
绕平面内某点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() (点
(点![]() 分别与
分别与![]() 点对应),若
点对应),若![]() 的两个顶点恰好落在抛物线上,请直接写出点
的两个顶点恰好落在抛物线上,请直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是“经过已知直线外一点作这条直线的平行线”的尺规作图过程.
己知:如图1,直线![]() 和直线
和直线![]() 外一点
外一点![]() .
.
求作:直线![]() 的平行直线,使它经过点
的平行直线,使它经过点![]() .
.

作法:如图2,
(1)过![]() 作直线
作直线![]() 与直线
与直线![]() 交于点
交于点![]() ;
;
(2)在直线![]() 取一点
取一点![]() ,以点
,以点![]() 为圆心,
为圆心,![]() 长为半径画弧,与直线
长为半径画弧,与直线![]() 交于点
交于点![]() ;
;
(3)以点![]() 为圆心,
为圆心,![]() 长为半径画弧,交直线
长为半径画弧,交直线![]() 于点
于点![]() 以点
以点![]() 为圆心,
为圆心,![]() 长为半径画弧,两弧交于点
长为半径画弧,两弧交于点![]() ;
;
(4)作直线![]() .
.
所以,直线![]() 就是所求作的平行线.
就是所求作的平行线.
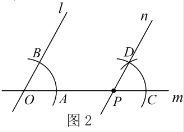
请回答:该作图的依据是______________________________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD中,点E是CD上一点(不与C,D两点重合),连接BE,过点C作CH⊥BE于点F,交对角线BD于点G,交AD边于点H,连接GE,
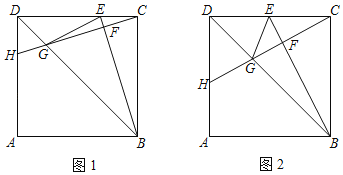
(1)求证:△DHC≌△CEB;
(2)如图2,若点E是CD的中点,当BE=8时,求线段GH的长;
(3)设正方形ABCD的面积为S1,四边形DEGH的面积为S2,当![]() 的值为
的值为![]() 时,
时,![]() 的值为 .
的值为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com