Question

14．如图1，在平面直角坐标系xOy中，直线EF：y=kx+3与x轴，y轴分别交点E，F，△OEF为等腰直角三角形．
（1）求k的值；
（2）菱形ABCD的顶点A的坐标为（2，0），点B的坐标为（0，1），点C在第一象限，对角线BD与x轴平行，将菱形ABCD沿x轴向左平移m个单位，当点D落在△EOF的内部时（不包括三角形的边），求m的取值范围；
（3）如图2，直线PQ：y=$\frac{1}{2}$x+2交x轴于点Q，点P（2，n），点M为PQ上一点，点S在x轴正半轴上，连接PS，过S作ST⊥PS，交y轴于点T，点G（-1，0），作射线MG交ST于点N，若PS=NS，求点M的坐标．

Answer 1

分析 （1）首先确定点F坐标（0，3），再利用等腰直角三角形的性质求出点E坐标，利用待定系数法即可解决问题；
（2）如图1中，连接AC交BD于K，延长DB交EF于G．求出点G、D的坐标，求出BD、BG即可解决问题；
（3）如图2中，连接PG、PN、PN交x轴于H，MN交y轴于D，作PC⊥x轴于C．只要证明△DOG是等腰直角三角形，求出直线DG的解析式，利用方程组求出点M坐标即可．

解答 解：（1）∵直线EF：y=kx+3与x轴，y轴分别交点E，F，
∴F（0，3），
∵△EOF是等腰直角三角形，
∴OE=OF=3，
∴E（-3，0）代入y=kx+3中，解得k=1，
∴k=1．

（2）如图1中，连接AC交BD于K，延长DB交EF于G．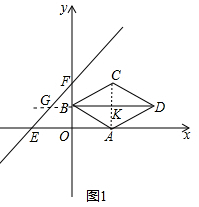

∵菱形ABCD的顶点A的坐标为（2，0），点B的坐标为（0，1），点C在第一象限，对角线BD与x轴平行，
∴AC⊥BD，BK=DK=2，D（4，1），G（-2，1），
∴BD=4，DG=6，
∴当4≤m≤6时，点D落在△EOF的内部．

（3）如图2中，连接PG、PN、PN交x轴于H，MN交y轴于D，作PC⊥x轴于C．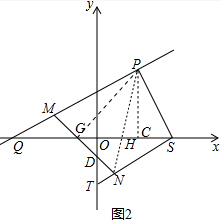

∵点P（2，n）在直线y=$\frac{1}{2}$x+2上，
∴P（2，3），∵G（-1，0），
∴PC=CG=3，
∴△PCG是等腰直角三角形，
∵△PNS是等腰直角三角形，
∴∠PGH=∠NHS=45°，∵∠GHP=∠NHS，
∴△PHG∽△SHN，
∴$\frac{GH}{HN}$=$\frac{PH}{SH}$，
∴$\frac{GH}{PH}$=$\frac{HN}{SH}$，∵∠PHS=∠GHN，
∴△PHS∽△GHN，
∴∠HPS=∠HGN=45°，
∴OG=OD=1，
∴D（0，-1），
∴A直线DM的解析式为y=-x-1，
由$\left\{\begin{array}{l}{y=-x-1}\\{y=\frac{1}{2}x+2}\end{array}\right.$，解得$\left\{\begin{array}{l}{x=-2}\\{y=1}\end{array}\right.$，
∴点M坐标为（-2，1）．

点评 本题考查一次函数综合题、等腰直角三角形的判定和性质、菱形的性质、相似三角形的判定和性质等知识，解题的关键是理解题意，灵活运用所学知识解决问题，学会添加常用辅助线，构造相似三角形解决问题，属于中考压轴题．