
| A. | $\sqrt{2}$ | B. | 4 | C. | 2 | D. | 2$\sqrt{2}$ |
分析 根据平行四边形的性质可知:对角线AB、CD互相平分,可得CD过线段AB的中点M,即CM=DM,根据A与B坐标求出M坐标,要求CD的最小值只需求出CM的最小值即可.
解答 解:根据平行四边形的性质可知:对角线AB、CD互相平分,
∴CD过线段AB的中点M,即CM=DM,
∵A(0,6),B(0,-4),
∴M(0,1),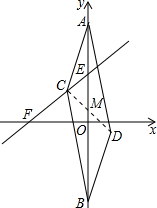
∵点到直线的距离垂线段最短,
∴过M作直线的垂线交直线于点C,此时CM最小,
直线x-y+3=0,令x=0得到y=3;令y=0得到x=-3,即F(-3,0),E(0,3),
∴OE=3,OF=3,EM=2,EF=$\sqrt{O{E}^{2}+O{F}^{2}}$=3$\sqrt{2}$,
∵△EOF∽△ECM,
∴$\frac{CM}{OF}=\frac{EM}{EF}$,
即$\frac{CM}{3}=\frac{2}{3\sqrt{2}}$,
解得:CM=$\sqrt{2}$,
则CD的最小值为2CM=2$\sqrt{2}$.
故选D.
点评 此题考查了平行四边形的判定与性质、相似三角形的判断和性质以及坐标与图形性质,熟练掌握平行四边形的判定与性质是解本题的关键.


科目:初中数学 来源: 题型:解答题
 已知抛物线y=ax2+bx经过点(3,-3),(-1,-3).
已知抛物线y=ax2+bx经过点(3,-3),(-1,-3).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (0,0) | B. | (a,-b) | C. | (-a,b) | D. | (-a,-b) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
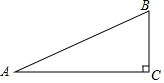 如图,在△ABC中,∠C=90°,BC=5,AB=13,则sinB是( )
如图,在△ABC中,∠C=90°,BC=5,AB=13,则sinB是( )| A. | $\frac{5}{13}$ | B. | $\frac{5}{12}$ | C. | $\frac{12}{13}$ | D. | $\frac{13}{12}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 王林同学利用暑假参观了幸福村果树种植基地(如图),他出发沿(1,3),(-3,3),(-4,0),(-4,-3),(2,-2),(5,-3),(5,0),(5,4)的路线进行了参观,请你按他参观的顺序写出他路上经过的地方,并用线段依次连接他经过的地点.
王林同学利用暑假参观了幸福村果树种植基地(如图),他出发沿(1,3),(-3,3),(-4,0),(-4,-3),(2,-2),(5,-3),(5,0),(5,4)的路线进行了参观,请你按他参观的顺序写出他路上经过的地方,并用线段依次连接他经过的地点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
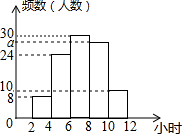 某校为了解清明假期全校同学参加课外活动的情况,抽查了100名同学,统计它们假期参加课外活动的时间并绘成频数分布直方图(如图),则参加课外活动时间的中位数所在的范围是( )
某校为了解清明假期全校同学参加课外活动的情况,抽查了100名同学,统计它们假期参加课外活动的时间并绘成频数分布直方图(如图),则参加课外活动时间的中位数所在的范围是( )| A. | 4-6小时 | B. | 6-8小时 | C. | 8-10小时 | D. | 10-12小时 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com