
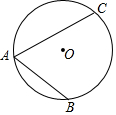
 如图,⊙O的半径为3cm,弦AC=4$\sqrt{2}$cm,AB=4cm,若以O为圆心,再作一个圆与AC相切,则这个圆的半径为多少?并判断这个圆与AB的位置关系.
如图,⊙O的半径为3cm,弦AC=4$\sqrt{2}$cm,AB=4cm,若以O为圆心,再作一个圆与AC相切,则这个圆的半径为多少?并判断这个圆与AB的位置关系. 分析 根据垂径定理和勾股定理可以求得点O到AC和AB的距离,从而可以解答本题.
解答 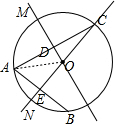 解:过点O作OM⊥AC于点D,作ON⊥AB于点E,如右图所示,
解:过点O作OM⊥AC于点D,作ON⊥AB于点E,如右图所示,
∵⊙O的半径为3cm,弦AC=4$\sqrt{2}$cm,AB=4cm,
∴OD=$\sqrt{O{A}^{2}-A{D}^{2}}=\sqrt{{3}^{2}-(2\sqrt{2})^{2}}=1$cm,
OE=$\sqrt{O{A}^{2}-A{E}^{2}}=\sqrt{{3}^{2}-{2}^{2}}=\sqrt{5}$,
∵1<$\sqrt{5}$,
∴如再作一个圆与AC相切,则这个圆的半径是1cm,这个圆与AB相离.
点评 本题考查切线的性质、垂径定理,解题的关键是明确题意,找出所求问题需要的条件.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
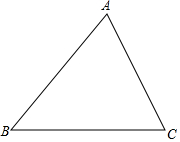 已知△ABC,利用位似变换,求作内接于已知△ABC的矩形DEFG,使它的边EF在BC上,顶点D,G分别在AB,AC上,且DE:EF=1:2(不写画法,保留画图痕迹).
已知△ABC,利用位似变换,求作内接于已知△ABC的矩形DEFG,使它的边EF在BC上,顶点D,G分别在AB,AC上,且DE:EF=1:2(不写画法,保留画图痕迹).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
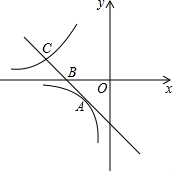 如图,直线y=-x+a与双曲线y=$\frac{4}{x}$(x<0)有唯一公共点A,与x轴于双曲线y=$\frac{k}{x}$(x<0)分别交于点B,C.
如图,直线y=-x+a与双曲线y=$\frac{4}{x}$(x<0)有唯一公共点A,与x轴于双曲线y=$\frac{k}{x}$(x<0)分别交于点B,C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
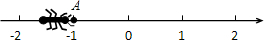 如图,一只蚂蚁从点A沿数轴向左直爬3个单位长度到达点B,点A表示-1,设点B所表示的数为m.
如图,一只蚂蚁从点A沿数轴向左直爬3个单位长度到达点B,点A表示-1,设点B所表示的数为m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 员工 | 经理 | 副经理 | 职员A | 职员B | 职员C | 职员D | 职员E | 职员F | 杂工G |
| 月工资/元 | 7000 | 4400 | 2400 | 2000 | 1900 | 1800 | 1800 | 1800 | 1200 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
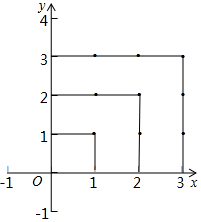 一个粒子在第一象限运动,在第一秒钟内它从原点运动到(1,0),而后它接着按图所示在与x轴、y轴平行的方向或在x轴、y轴上来回运动,且每秒移动1个单位长度.
一个粒子在第一象限运动,在第一秒钟内它从原点运动到(1,0),而后它接着按图所示在与x轴、y轴平行的方向或在x轴、y轴上来回运动,且每秒移动1个单位长度.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com