练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    按要求作图（本题5分）（不写作法，但要保留作图痕迹）

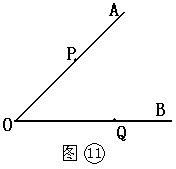    已知点P、Q分别在∠AOB的边OA，OB上（如图 ⑾   ）.

    ① 作直线PQ，

    ② 过点P作OB的垂线PC，

    ③ 过点Q作OA的平行线QD.

     

    【答案】

    见解析

     【解析】此题考查学生的基本作图能力。                                            

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    按要求作图（本题5分）（不写作法，但要保留作图痕迹）

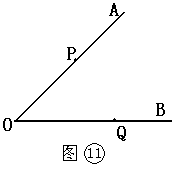    已知点P、Q分别在∠AOB的边OA，OB上（如图⑾   ）.

    ① 作直线PQ，

    ② 过点P作OB的垂线PC，

    ③ 过点Q作OA的平行线QD.

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    (本题9分)如图，△ABC是直角三角形，∠ACB=90°．

    （1）实践与操作 利用尺规按下列要求作图，并在图中标明相应的字母(保留作图痕迹，不写作法)．

    ①作△ABC的外接圆，圆心为O；

    ②以线段AC为一边，在AC的右侧作等边△ACD；

    ③连接BD，交⊙O于点F，连接AE，

    (2)综合与运用  在你所作的图中，若AB=4，BC=2，则：

    ①AD与⊙O的位置关系是______．(2分)

    ②线段AE的长为__________．(2分)

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    (本题9分)如图，△ABC是直角三角形，∠ACB=90°．
    （1）实践与操作利用尺规按下列要求作图，并在图中标明相应的字母(保留作图痕迹，不写作法)．
    ①作△ABC的外接圆，圆心为O；
    ②以线段AC为一边，在AC的右侧作等边△ACD；
    ③连接BD，交⊙O于点F，连接AE，
    (2)综合与运用 在你所作的图中，若AB=4，BC=2，则：
    ①AD与⊙O的位置关系是______．(2分)
    ②线段AE的长为__________．(2分)

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    观察可得最简公分母是(x＋1)(x－1)，方程两边乘最简公分母，可以把分式方程转化为整式方程求解．

    【解答】

    （2）方程的两边同乘(x＋1)(x－1)，得

    2(x－1)＋4＝x2－1，

    即x2－2x－3＝0，

    (x－3)(x＋1)＝0，

    解得x1＝3，x2＝－1，

    检验：把x＝3代入(x＋1)(x－1)＝8≠0，即x＝3是原分式方程的解，

    把x＝－1代入(x＋1)(x－1)＝0，即x＝－1不是原分式方程的解，

    则原方程的解为：x＝3．

    【点评】此题考查了实数的混合运算与分式方程的解法．此题难度不大，但注意掌握绝对值的性质、负指数幂的性质、零指数幂的性质以及特殊角的三角函数值，注意解分式方程一定要验根．

    20．（本题满分5分）如图，已知△ABC，且∠ACB＝90°。

    （1）请用直尺和圆规按要求作图（保留作图痕迹，不写作法和证明）；

    ①以点A为圆心，BC边的长为半径作⊙A；

    ②以点B为顶点，在AB边的下方作∠ABD=∠BAC．

    （2）请判断直线BD与⊙A的位置关系（不必证明）．

     


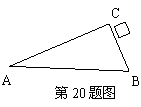    查看答案和解析>>

    同步练习册答案